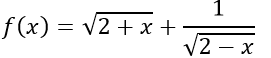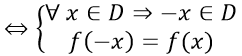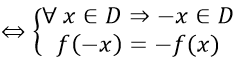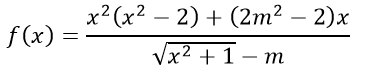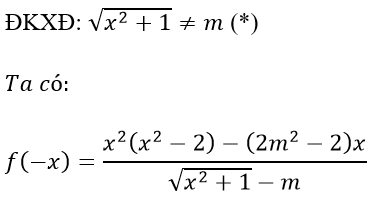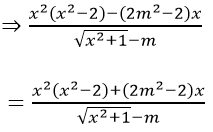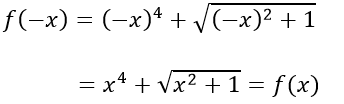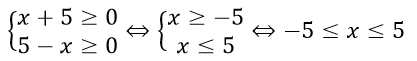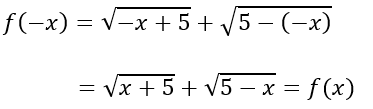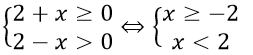Cách xét tính chẵn lẻ của hàm số hay, chi tiết

1. Phương pháp giải.

* Sử dụng định nghĩa

Hàm số y = f(x) xác định trên D

    + Hàm số chẵn 

    + Hàm số lẻ 

Chú ý: Một hàm số có thể không chẵn cũng không lẻ

        Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng

        Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng

* Quy trình xét hàm số chẵn, lẻ.

B1: Tìm tập xác định của hàm số.

B2: Kiểm tra

    Nếu ∀ x ∈ D ⇒ -x ∈ D Chuyển qua bước ba

    Nếu ∃ x₀ ∈ D ⇒ -x₀ ∉ D kết luận hàm không chẵn cũng không lẻ.

B3: xác định f(-x) và so sánh với f(x).

    Nếu bằng nhau thì kết luận hàm số là chẵn

    Nếu đối nhau thì kết luận hàm số là lẻ

    Nếu tồn tại một giá trị ∃ x₀ ∈ D mà f(-x₀ ) ≠ ± f(x₀) kết luận hàm số không chẵn cũng không lẻ.

2. Các ví dụ minh họa.

Ví dụ 1: Tìm m để hàm số sau là hàm số chẵn.

Hướng dẫn:

Giả sử hàm số chẵn suy ra f(-x) = f(x) với mọi x thỏa mãn điều kiện (*)

với mọi x thỏa mãn (*)

⇒ 2(2m² - 2) x = 0 với mọi x thỏa mãn (*)

⇔ 2m² - 2 = 0 ⇔ m = ± 1

+ Với m = 1 ta có hàm số là

ĐKXĐ : √(x²+1) ≠ 1 ⇔ x ≠ 0

Suy ra TXĐ: D = R\{0}

Dễ thấy với mọi x ∈ R\{0} thì -x ∈ R\{0} và f(-x) = f(x)

Do đó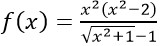là hàm số chẵn.

+ Với m = -1 ta có hàm số là

TXĐ: D = R

Dễ thấy với mọi x ∈ R thì -x ∈ R và f(-x) = f(x)

Do đó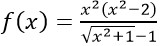là hàm số chẵn.

Vậy m = ± 1 là giá trị cần tìm.

Ví dụ 2: Xét tính chẵn, lẻ của các hàm số sau:

Hướng dẫn:

a) f(x) = 3x³ + 2∛x

TXĐ: D = R.

Với mọi x ∈ D, ta có -x ∈ D

f(-x) = 3.(-x)³ + 2∛(-x) = -(3x³ + 2∛x) = -f(x)

Do đó f(x) = 3x³ + 2∛x là hàm số lẻ

b)

TXĐ: D = R.

Với mọi x ∈ D, ta có -x ∈ D

Do đó 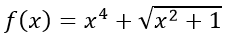 là hàm số chẵn

c)

ĐKXĐ:

Suy ra TXĐ: D = [-5;5]

Với mọi x ∈ [-5;5] ta có -x ∈ [-5;5]

Do đó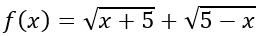là hàm số chẵn

d)

ĐKXĐ:

Suy ra TXĐ: D = [-2; 2)

Ta có x₀ = -2 ∈ D nhưng -x₀ = 2 ∉ D

Vậy hàm sốkhông chẵn và không lẻ.