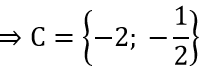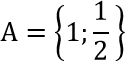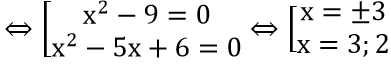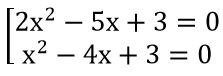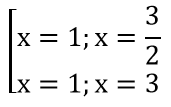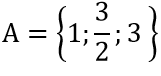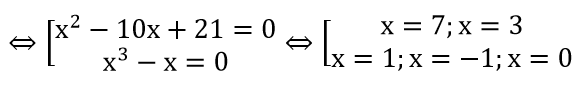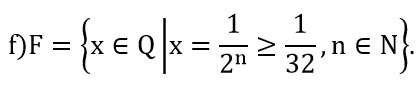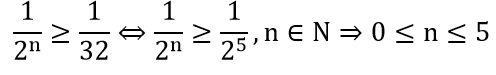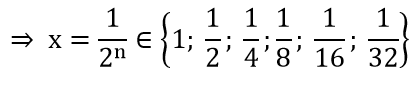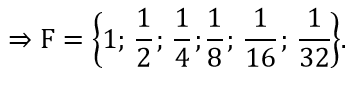Bài tập Tập hợp và các phép toán trên tập hợp chọn lọc, có lời giải
Bài tập Tập hợp và các phép toán trên tập hợp chọn lọc, có lời giải Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Bài tập Tập hợp và các phép toán trên tập hợp chọn lọc, có lời giải
Bài tập Tập hợp và các phép toán trên tập hợp chọn lọc, có lời giải
Bài 1: Cho các tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 2, 3, 4};
C = {2, 4, 6, 8}. Hãy xác định: CA B; CA C;CA (B ∪ C).

Bài 2: Viết các tập sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {0; 1; 2; 3; 4}
b) B ={ -3; 9; -27; 81}
e) E = Tập tất cả các điểm thuộc đường trung trực của đoạn thẳng AB.
f) F = Tập tất cả các điểm thuộc đường tròn tâm I cho trước và có bán kính bằng 5.
Bài 3: Cho biết mỗi tập hợp sau có bao nhiêu tập hợp con, tìm tất cả các tập hợp con của tập hợp sau:
a) A = {1; 2}
b) B = {1; 2; 3}
c) C={x ∈ R|2x2-5x+2=0}
d) D={x ∈ Q|x2-4x+2=0}
Bài 4: Trong các tập hợp sau, tập nào là tập con của tập nào?
a)
| A = {1; 2; 3}, | B ={x ∈ N|x < 4}, |
| C ={0; +∞}, | D ={x ∈ R|2x2 - 7x + 3 = 0} |
b)
| A = Tập các ước số tự nhiên của 6; | B = Tập các ước số tự nhiên của 12; |
c)
| A = Tập các hình bình hành; | B = Tập các hình chữ nhật; |
| C = Tập các hình thoi; | D = Tập các hình vuông, |
d)
| A = Tập các tam giác cân; | B = Tập các tam giác đều; |
| C = Tập các tam giác vuông; | D = Tập các tam giác vuông cân. |
Bài 5: Tìm A ∩ B;A ∪ B;A\B;B\A với
a) A={2,4,7,8,9,12};B={2,8,9,12}.
b) A={x ∈ Q|2x2 - 3x + 1 = 0};B={x ∈ R||2x - 1|= 1}
c) A = Tập các ước số của 12; B = Tập hợp các ước số của 18.
d) A={x ∈ N|(x2 - 9)(x2 - 5x + 6 = 0}; B = Tập các số nguyên tố có 1 chữ số.
Bài 6: Xác định các tập hợp A, B sao cho:
A ∩ B ={0,1,2,3,4}; A \ B ={-3,-2};B \ A ={6,9,10}.
Bài 7: Mỗi học sinh lớp 10A đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn thể thao này. Hỏi lớp 10A có bao nhiêu học sinh?
Bài 8: Kết quả điều tra ở một lớp cho thấy: có 20 hoc sinh thích bóng đá, 17 học sinh thích bơi, 36 học sinh thích chơi bóng chuyền, 14 học sinh thích bóng đá và bơi, 13 học sinh thích bơi và bóng chuyền, 15 học sinh thích bóng đá và bóng chuyền, 10 học sinh thích cả ba môn, 12 học sinh không thich môn nào. Tính xem lơp học có bao nhiêu học sinh?
Bài 9: Trong 100 học sinh lớp 10, có 70 học sinh nói được tiếng Anh, 45 học sinh nói được tiếng Pháp và 23 học sinh nói được cả hai tiếng Anh và Pháp. Hỏi có bao nhiêu học sinh không nói được cả hai tiếng Anh và Pháp.
Bài 10: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó
a) A={x ∈ R|(2x2 - 5x + 3)(x2 - 4x + 3)= 0}.
b) B={x ∈ R|(x2 - 10x + 21)(x3 - x)= 0}.
c) C={x ∈ N|x + 3 < 4 + 2x; 5x - 3 < 4x - 1}.
d) D={x ∈ Z||x + 2| ≤ 3}.
e) E={x ∈ R|x2 + x + 3 = 0}.
Đáp án và hướng dẫn giải
Bài 1: A = {1, 2, 3, 4, 5, 6, 7, 8, 9}; B = {1, 2, 3, 4};
C = {2, 4, 6, 8}.
CA B={5,6,7,8,9}; CA C={1,3,5,7,9}
B ∪ C={1, 2, 3, 4, 6, 8} ⇒ CA (B ∪ C)={5;7;9}
Bài 2: Viết các tập sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:
a) A = {0; 1; 2; 3; 4}
A={x ∈ N|x ≤ 4}
b) B ={ -3; 9; -27; 81}
B={x ∈ Z|x=(-3)n ;n < 5;n ∈ N}
e) E = Tập tất cả các điểm thuộc đường trung trực của đoạn thẳng AB.
E = Tập tất cả các điểm cách đều hai đầu mút A và B
Hay E = Tập tất cả các điểm I sao cho IA = IB.
f) F = Tập tất cả các điểm thuộc đường tròn tâm I cho trước và có bán kính bằng 5.
F = Tập tất cả các điểm cách điểm I một khoảng bằng 5.
Bài 3: Cho biết mỗi tập hợp sau có bao nhiêu tập hợp con, tìm tất cả các tập hợp con của tập hợp sau:
a) A = {1; 2}
A có 2 phần tử nên A có 22 = 4 tập con
Các tập hợp con của A là: {1;2}; {1}; {2}; ∅ .
b) B = {1; 2; 3}
B có 3 phần tử nên A có 23 = 8 tập con
Các tập hợp con của B là: {1; 2; 3} {1;2};{1;3}; {2;3}; {1}; {2};{3}; ∅ .
c) C={x ∈ R|2x2 - 5x + 2 = 0}
2x2 - 5x + 2 = 0 ⇔ x = -2;
C có 2 phần tử nên C có 22 = 4 tập con
Các tập hợp con của C là: 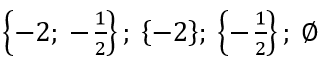
d) D={x ∈ Q|x2 - 4x + 2 = 0}
x2 - 4x + 2 = 0 ⇔ x = 2 ± √2
Do x ∈ Q nên D = ∅ .
Do đó, D có 1 tập con là chính nó.
Bài 4:
| a) A = {1; 2; 3}, | B={x ∈ N|x < 4}, |
| C={0; +∞}, | D={x ∈ R|2x2 - 7x + 3 = 0} |
Ta có: B={x ∈ N|x < 4} ⇒ B={0;1 ;2;3}
D={x ∈ R|2x2 - 7x + 3 = 0} ⇒ 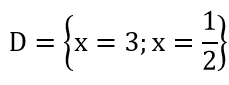
Khi đó: A ⊂ B ⊂ C và D ⊂ C.
b) A = Tập các ước số tự nhiên của 6 ⇒ A={1;2;3;6}
B = Tập các ước số tự nhiên của 12 ⇒ B={1;2;3;4;6;12}
Khi đó A ⊂ B
c)
| A = Tập các hình bình hành; | B = Tập các hình chữ nhật; |
| C = Tập các hình thoi; | D = Tập các hình vuông, |
Ta có: D ⊂ B ⊂ A và D ⊂ C
d)
| A = Tập các tam giác cân; | B = Tập các tam giác đều; |
| C = Tập các tam giác vuông; | D = Tập các tam giác vuông cân. |
Ta có: B ⊂ A; D ⊂ C, D ⊂ A.
Bài 5: Tìm A ∩ B;A ∪ B;A \ B;B \ A với
a) A={2,4,7,8,9,12};B={2,8,9,12}.
A ∩ B={2;8;9;12}; A ∪ B={2,4,7,8,9,12};
A\B={4;7}; B \ A = ∅ .
b) A={x ∈ Q|2x2 - 3x + 1 = 0};B={x ∈ R||2x - 1|= 1}
2x2 - 3x + 1 = 0⇔x=1;x=1/2 ⇒
|2x - 1|= 1 ⇔ x = 0; x = 1 ⇒ B ={0;1 }
A ∩ B = {1};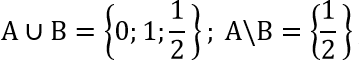
c) A = Tập các ước số của 12 ⇒ A={1;2;3;4;6;12}
B = Tập hợp các ước số của 18 ⇒ B={1;2;3;6;9;18}
A ∩ B={1;2;3;6}; A ∪ B={1;2;3;4;6;9;12;18}
A \ B={4;12}; B \ A={9;18}
d) A={x ∈ N|(x2 - 9)(x2 - 5x + 6 = 0};
(x2 - 9)(x2 - 5x + 6)= 0
⇒ A={-3;2;3}
B = Tập các số nguyên tố có 1 chữ số.
B={2;3;5;7}
A ∩ B={2;3}; A ∪ B={-3;2;3;5;7}; A \ B={-3};B \ A={5;7}.
Bài 6:
a) A ∩ B={0,1,2,3,4}; A\B={-3,-2};B\A={6,9,10}.
A ∩ B={0,1,2,3,4} ⇒ 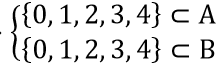
A\B={-3,-2} ⇒ 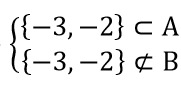
B\A={6,9,10} ⇒ 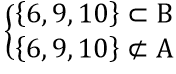
⇒ A={0,1,2,3,4} ∪ {-3,-2}={-3,-2,0,1,2,3,4 }
B={0,1,2,3,4} ∪ {6,9,10}={0,1,2,3,4,6,9,10}
Bài 7:
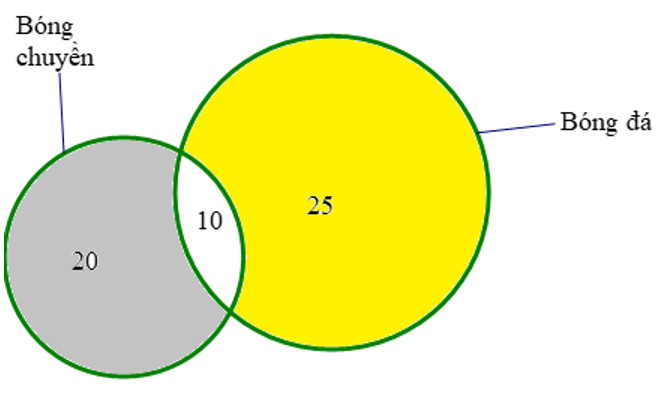
Từ sơ đồ ta thấy: Số học sing của lớp 10A là: 25 + 20 – 10 = 35 (học sinh)
Bài 8:
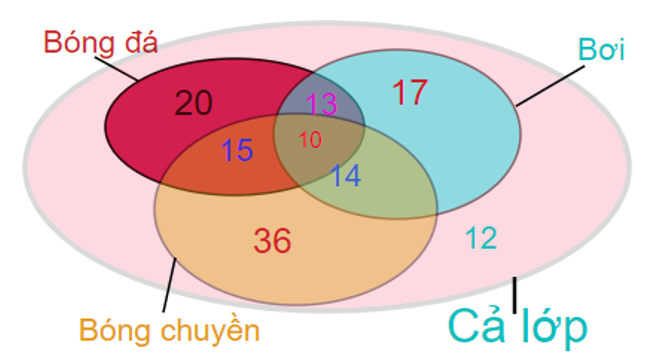
Từ sơ đồ trên, ta có:
Số học sinh của cả lớp là:
20 + 17 + 36 - (13 + 14 + 15) + 10 = 53 (học sinh)
Bài 9:
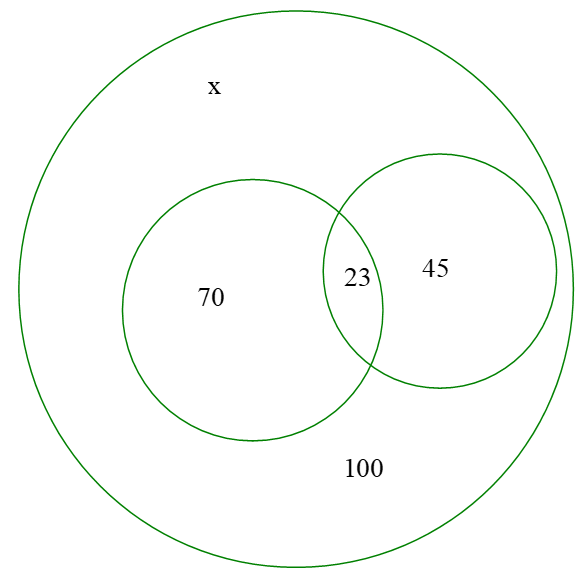
Gọi số học sinh không nói được cả Tiếng Anh và tiếng Pháp là x
x + 70 + 45 - 23 = 100 ⇒ x=8 học sinh.
Bài 10: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó
a) (2x2-5x+3)(x2-4x+3)=0⇔
⇔
⇒
b) (x2 - 10x + 21)(x3 - x)=0
⇒ B={-1;0;1;3;7 }.
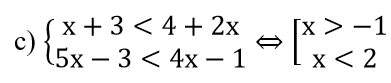
⇒ C={0;1}
d) D={x ∈ Z||x + 2| ≤ 3}.
|x + 2| ≤ 3 ⇔ -3 < x + 2 < 3 ⇔ - 5 < x < 1
⇒ D={-4; -3; -2; -1;0}
e)E={x ∈ R|x2 + x + 3 = 0}.
x2 + x + 3 = 0: Phương trình này vô nghiệm do đó E = ∅