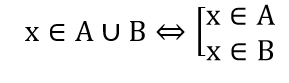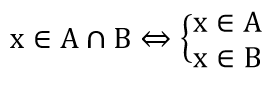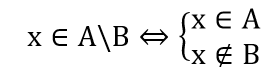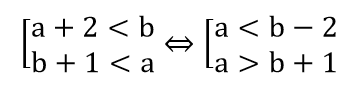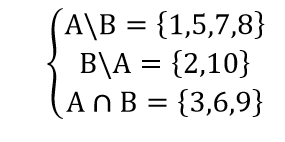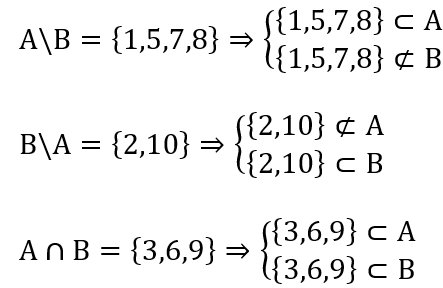Phương pháp giải

Hợp của 2 tập hợp:

x ∈ A ∪ B ⇔

Giao của 2 tập hợp

x ∈ A ∩ B ⇔

Hiệu của 2 tập hợp

x ∈ A \ B ⇔

Phần bù

Khi B ⊂ A thì A\B gọi là phần bù của B trong A, kí hiệu là C_A B.

Ví dụ minh họa

Ví dụ 1:

Cho hai đoạn A=[a ;a + 2 ] và B=[b ;b + 1]. Các số a và b cần thỏa mãn điều kiện gì để A ∩ B≠ ∅

Hướng dẫn:

Điều kiện để A ∩ B= ∅ là:

Từ đó, suy ra điều kiện để A ∩ B ≠ ∅ là b-2 ≤ a ≤ b + 1

Ví dụ 2: Cho hai tập hợp:

A = { x ∈ R | x² - 4x + 3 = 0};

B = { x ∈ R | x² - 3x + 2 = 0}.

Tìm A ∪ B ; A ∩ B ; A \ B ; B \ A.

Hướng dẫn:

Ta có: A={1;3} và B={1;2}

A ∪ B={1;2;3}

A ∩ B={1}

A \ B={3}

B \ A={2}

Ví dụ 3: Cho đoạn A=[-5;1] và khoảng B =(-3; 2). Tìm A ∪ B; A ∩ B.

Hướng dẫn:

A ∪ B=[-5;2)

A ∩ B=(-3;1]

Ví dụ 4: Cho A={1,2,3,4,5,6,9}; B={1,2,4,6,8,9} và C={3,4,5,6,7}

a) Tìm hai tập hợp (A \ B) ∪ (B \ A) và (A ∪ B) \\ (A ∩ B). Hai tập hợp nhận được có bằng nhau không?

b) Hãy tìm A ∩ (B \ C) và (A ∩ B) \ C. Hai tập hợp nhận được có bằng nhau không?

Hướng dẫn:

a) A \ B={3,5}; B \ A={8}

⇒ (A \ B) ∪ (B \ A)={3;5;8}

A ∪ B={1,2,3,4,5,6,8,9}

A ∩ B={1,2,4,6,9}

⇒ (A ∪ B) \\ (A ∩ B)= {3;5;8}

Do đó: (A \ B) ∪ (B \ A)=(A ∪ B) \\ (A ∩ B)

b) B \ C={1,2,8,9}

⇒ A ∩ (B \ C) ={1,2,9}.

A ∩ B={1,2,4,6,9}

⇒ (A ∩ B) \ C ={1,2,9}.

Do đó A ∩ (B \ C) =(A ∩ B) \ C

Ví dụ 5: Tìm tập hợp A, B biết:

Hướng dẫn:

⇒ A = {1,5,7,8} ∪ {3,6,9} = {1,3,5,6,7,8,9}

B={2,10} ∪ {3,6,9} = {2,3,6,9,10}

Ví dụ 6: Cho A là tập hợp các học sinh lớp 10 đang học ở trường em và B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B;A ∩ B;A \ B;B \ A.

Hướng dẫn:

1. A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.

2. A ∩ B: tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.

3. A \ B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.

4. B \ A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.