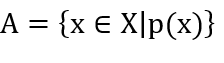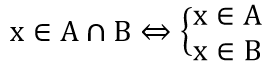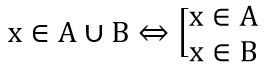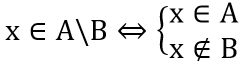Lý thuyết Tập hợp và các phép toán trên tập hợp hay, chi tiết
Lý thuyết Tập hợp và các phép toán trên tập hợp hay, chi tiết Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Lý thuyết Tập hợp và các phép toán trên tập hợp hay, chi tiết
Lý thuyết Tập hợp và các phép toán trên tập hợp hay, chi tiết
1. Tập hợp- Phần tử
+ Tập hợp, phần tử là những khái niệm cơ bản của toán học.
Các đối tượng có chung một hay nhiều tính chất quy tụ lại thành một tập hợp; mỗi đối tượng là một phần tử.
+ Mỗi tập hợp được xác định bởi:
- Liệt kê các phần tử của nó: A={a1; a2; a3;…}
- Chỉ ra các tính chất đặc trưng cho các phần tử của nó: 
2. Tập hợp rỗng
Tập hợp rỗng, kí hiệu là ∅ , là tập hợp không chứa phần tử nào.
A ≠ ∅ ⇔ ∃x : x ∈ A
3. Tập hợp con
Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B, kí hiệu là A ⊂ B.
A ⊂ B ⇔ ∀x : x ∈ A ⇒ x ∈ B.
A ⊄ B ⇔ ∀x : x ∈ A ⇒ x ∉ B.
Tính chất:
1) A ⊂ A với mọi tập A.
2) Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
3) ∅ ⊂ A với mọi tập hợp A.
4.Tập hợp bằng nhau.
Khi A ⊂ B và B ⊂ A thì ta nói tập hợp A bằng tập hợp B và viết là A = B.
A = B ⇔(∀x : x ∈ A ⇔ x ∈ B )
5. Giao của hai tập hợp
Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.
6. Hợp của hai tập hợp
Tập hợp C gồm các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B.
7. Hiệu và phần bù của hai tập hợp
Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B.
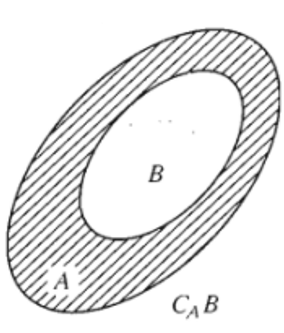
Khi B ⊂ A thì tất các phần tử thuộc A mà không là phần tử của B (A\B) gọi là phần bù của B trong A, kí hiệu CA B (phần gạch chéo trong hình).
8. Các tập hợp con thường dùng của R
Khoảng:
(a;b)={x ∈ R|a < x < b}
(a;+∞)={x ∈ R|a < x}
(-∞;b)={x ∈ R|x < b}
Đoạn:
[a;b]={x ∈ R|a ≤ x ≤ b}
Nửa khoảng:
[a;b)={x ∈ R |a ≤ x < b}
(a;b]={x ∈ R |a < x ≤ b}
[a;+∞)={ x ∈ R | a ≤ x}
(-∞;b]={ x ∈ R | x ≤ b}
