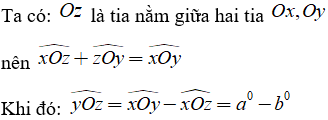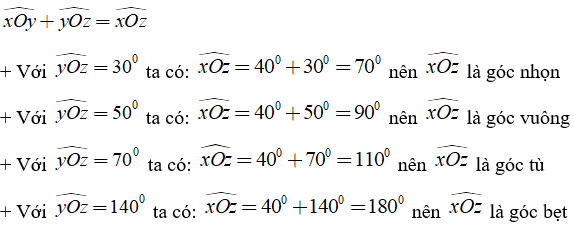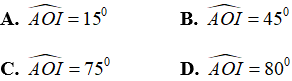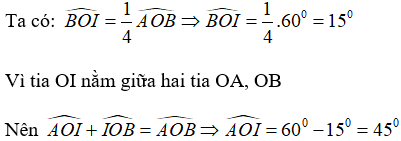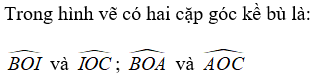Bài 64: Khi nào thì xOy + yOz = xOz

A. Lý thuyết

1. Khi nào thì tổng số đo hai góc góc xOy và yOz bằng số đo góc xOz

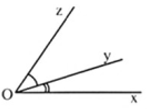
Nếu tia Oy nằm giữa hai tia Ox và Oy thì ∠xOy + ∠yOz = ∠xOz

Ngược lại, nếu ∠xOy + ∠yOz = ∠xOz thì tia Oy nằm giữa hai tia Ox và Oy

2. Hai góc kề nhau, phụ nhau, kề bù

a. Hai góc kề nhau

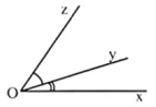
   + Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng chứa cạnh chung

   + Hai góc ∠xOy và ∠xOy là hai góc kề nhau vì có cạnh Oy chung và hai cạnh Ox; Oz nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng chứa tia Oy

b. Hai góc phụ nhau

Hai góc phụ nhau là hai góc có tổng số đo bằng 90^o

Ví dụ:

Nếu ∠A = 30^o và ∠B = 60^o thì ∠A và ∠B là hai góc phụ nhau ( vì ∠A + ∠B = 180^o )

c. Hai góc bù nhau

Hai góc bù nhau là hai góc có tổng số đo bằng 180^o

d. Hai góc kề bù

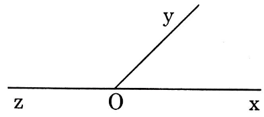
   + Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau ( hai góc có 1 cạnh chung và 2 cạnh 2 cạnh còn lại là 2 tia đối nhau)

   + Hai góc xOy và yOz trên hình vẽ vẽ là hai góc kề bù vì có cạnh Oy chung và hai cạnh Ox và Oz là hai tia đối nhau.

3. Chú ý

   + Với bất kì số m nào, 0^o ≤ m ≤ 180^o trên nửa mặt phẳng có bờ là đường thẳng chứa tia Ox bao giờ cũng vẽ được một và chỉ một tia Oy sao cho ∠xOy = m (độ )

   + Nếu có các tia Oy; Oz thuộc cùng một nửa mặt phẳng bờ chứa tia Ox và ∠xOy < ∠xOz thì tia Oy nằm giữa hai tia Ox và Oy

   + Hai góc cùng phụ (hoặc cùng bù) với một góc thứ ba thì bằng nhau

4. Ví dụ

Ví dụ 1: Gọi Oz là tia nằm giữa hai tia Ox, Oy . Biết 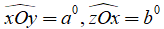 . Tính 

Hướng dẫn giải:

Ví dụ 2: Tia Oy nằm giữa hai tia Ox và Oz . Biết 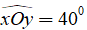 . Hỏi góc xOz là góc nhọn, vuông, tù hay bẹt nếu số đo của góc yOz lần lượt là 30°, 50°, 70°, 140° ?

Hướng dẫn giải:

Ta có: Tia Oy nằm giữa hai tia Ox và Oz nên :

5. Bài tập tự luyện

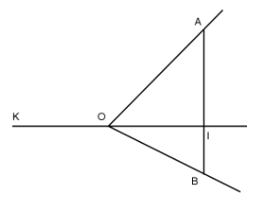
Câu 1: Ở hình, hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết ∠KOA = 120°, ∠BOI = 45°. Tính ∠KOB, ∠AOI, ∠BOA

Hướng dẫn giải:

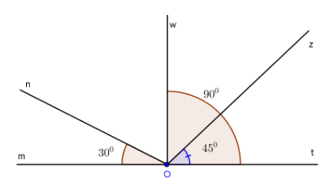
Câu 2: Cho hình vẽ

a) Gọi tên các cặp góc kề nhau tại đỉnh O trong hình vẽ

b) Cho biết số đo các góc tại đỉnh O

c) Cho biết những cặp góc phụ nhau tại đỉnh O

Hướng dẫn giải:

a) Các cặp góc kề nhau tại đỉnh O là: ∠mOn và ∠nOw; ∠mOn và ∠nOz; ∠mOn và ∠nOt; ∠mOw và ∠zOw;

∠mOw và ∠tOw; ∠mOz và ∠zOt; ∠wOn và ∠zOw; ∠wOn và ∠tOw; ∠wOz và ∠zOt.

b) Số đo các góc ở đỉnh O là: ∠mOt = 180°; ∠mOw = 90°; ∠nOw = 60°; ∠wOz = 45°

c) Các cặp góc phụ nhau tại đỉnh O là: ∠mOn và ∠nOw; ∠wOz và ∠zOt.

B. Bài tập trắc nghiệm

Câu 1: Chọn phát biểu đúng trong các phát biểu sau:

A. Hai góc tù là hai góc kề nhau

B. Cho ba tia chung gốc Ox, Oy, Oz, ta luôn có: ∠xOy + ∠yOz = ∠xOz

C. Nếu tia Oy nằm giữa hai tia On và Om thì khi đó ta có: ∠yOn + ∠yOm = ∠mOn

D. Nếu ∠A và ∠B là hai góc bù nhau thì ∠A + ∠B = 90°

Đáp án

Câu 2: Chọn câu sai trong các câu sau:

A. Nếu tia Ot nằm giữa hai tia Ou và Ov thì ∠tOu + ∠tOv = ∠uOv

B. Nếu hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng chứa cạnh chung thì hai góc đó kề nhau

C. Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc phụ nhau

D. Hai góc kề bù có tổng là 180°

Đáp án

Câu 3: Trên cùng một nửa mặt phẳng bờ là tia Ox có ∠xOy = 30°, ∠xOz = 65°, chọn phát biểu đúng trong các phát biểu sau:

A. Tia Ox nằm giữa hai tia Oy và Oz

B. Tia Oy nằm giữa hai tia Oz và Ox

C. Tia Oz nằm giữa hai tia Oy và Ox

D. Chưa thể kết luận được tia nào nằm giữa hai tia còn lại

Đáp án

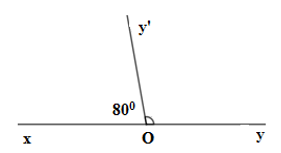
Câu 4: Cho ∠xOy và ∠yOy' là hai góc kề bù. Biết ∠xOy = 80°, số đo của ∠yOy' là:

A. 100°     B. 70°     C. 80°     D. 60°

Đáp án

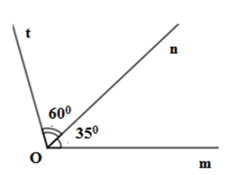
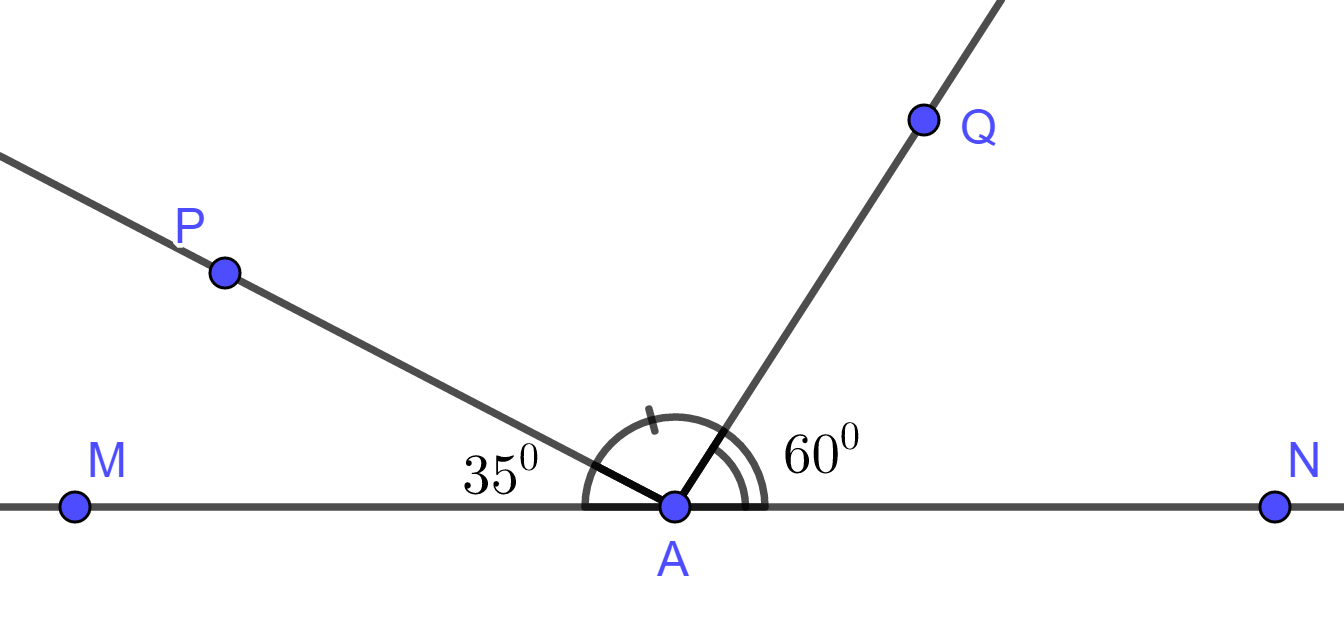
Câu 5: Cho hình vẽ:

Số đo của ∠tOm là:

A. 105°     B. 100°     C. 115°     D. 95°

Đáp án

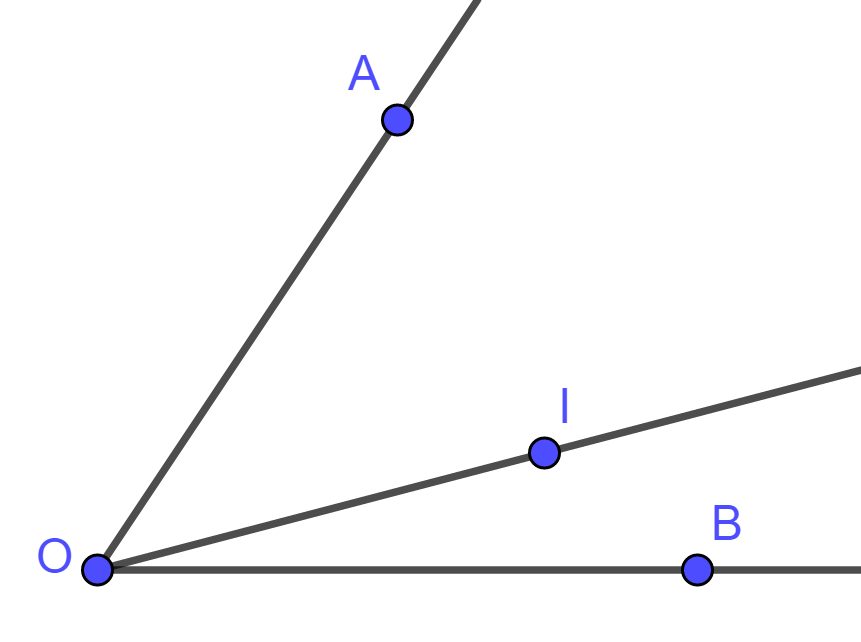
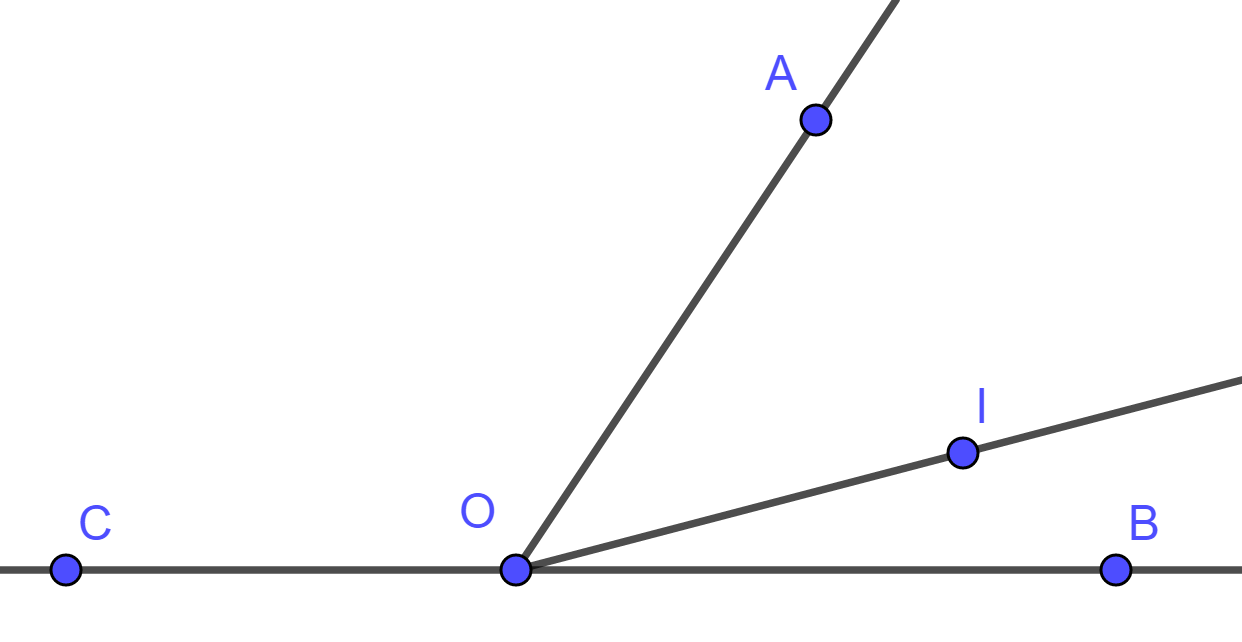
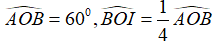
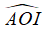
Câu 6: Cho hình vẽ sau, biết tia OI nằm giữa hai tia OA, OB,  . Số đo góc  ?

Đáp án

Câu 7: Cho hình vẽ sau. Có tất cả bao nhiêu cặp góc kề bù ở hình trên?

A. 1

B. 2

C. 3

D. 4

Đáp án

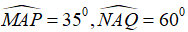
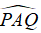
Câu 8: Cho hình vẽ sau biết hai tia AM và AN đối nhau,  , tia AQ nằm giữa hai tia AN và AP. Hãy tính số đo góc  .

A. 145°

B. 120°

C. 85°

D. 65°

Đáp án

Câu 9: Cho hình vẽ sau. Cặp góc phụ nhau là:

Đáp án

Câu 10: Trong các khẳng định sau, khẳng định đúng là?

A. Hai góc phụ nhau mà một góc là 450 thì góc kia là 1350

B. Hai góc bù nhau mà một góc là 450 thì góc kia là 450

C. Hai góc vuông là hai góc kề bù

D. Hai góc kề bù là hai góc có một cạnh chung và tia đối của góc này là tia của góc kia

Đáp án