Toán lớp 6 Bài 36: Đường thẳng đi qua hai điểm
Lý thuyết tổng hợp Toán học lớp 6 Bài 36: Đường thẳng đi qua hai điểm chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 6. Hy vọng bộ tổng hợp lý thuyết Toán lớp 6 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 6.
Bài 36: Đường thẳng đi qua hai điểm
A. Lý thuyết
1. Vẽ đường thẳng
Muốn vẽ đường thẳng đi qua hai điểm A và B ta làm như sau:
• Đặt cạnh thước đi qua hai điểm A và B;
• Dùng đầu chì vạch theo cạnh thước.
Nhận xét: Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm A và B
2. Tên đường thẳng
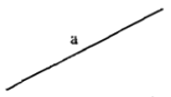
• Đặt tên đường thẳng bằng một chữ cái thường.
Ví dụ: Đường thẳng a, b, m, p,…
• Đặt tên đường thẳng bằng cách lấy tên hai điểm mà đường thẳng đi qua
Ví dụ: Đường thẳng AB, …
• Dùng hai chữ cái thường
3. Đường thẳng trùng nhau, cắt nhau, song song
Hai đường thẳng a, b bất kỳ có thể:
• Trùng nhau: Có vô số điểm chung.
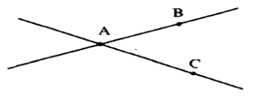
• Cắt nhau: Chỉ có một điểm chung – điểm chung đó gọi là giao điểm.
• Song song: Không có điểm chung nào.
Chú ý:
• Hai đường thẳng không trùng nhau còn được gọi là hai đường thẳng phân biệt.
• Hai đường thẳng phân biệt hoặc chỉ có một điểm chung hoặc không có điểm chung nào.

4. Bài tập tự luyện
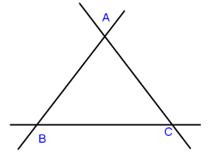
Câu 1: Cho ba đường A, B, C không thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm
a) Kẻ được mấy đường thẳng tất cả?
b) Viết tên các đường thẳng đó
c) Viết tên nút giao điểm của từng cặp đường thẳng
Hướng dẫn giải:
a) Vẽ được 3 đường thẳng tất cả
b) Tên các đường thẳng
+ Đường thẳng AB
+ Đường thẳng AC
+ Đường thẳng BC
c)
+ Giao điểm của đường thẳng AB và đường thẳng AC là điểm A.
+ Giao điểm của đường thẳng AB và đường thẳng BC là điểm B.
+ Giao điểm của đường thẳng BC và đường thẳng AC là điểm C.
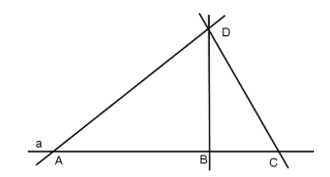
Câu 2: Vẽ đường thẳng a, lấy A ∈ a; B ∈ a; C ∈ a; D ∉ a. Kẻ các đường thẳng đi qua các cặp điểm
a) Kẻ được tất cả bao nhiêu đường thẳng phân biệt
b) Viết tên các đường thẳng đó.
c) D là giao điểm của những đường thẳng nào?
Hướng dẫn giải:
a)
Có 4 đường thẳng phân biệt
b) Tên các đường thẳng đó
+ Đường thẳng AD
+ Đường thẳng DC
+ Đường thẳng BD
+ Đường thẳng a.
c) D là giao điểm của 3 đường thẳng AD, DC, DB
Ta nói: Ba đường thẳng AD, DC, DB đồng quy tại điểm D.
B. Bài tập trắc nghiệm
Câu 1: Cho hai đường thẳng a, b. Khi đó a, b có thể:
A. Song song B. Trùng nhau
C. Cắt nhau D. Cả ba đáp án trên đều đúng
Đáp án
Hai đường thẳng a, b bất kỳ có thể trùng nhau, song song hoặc cắt nhau.
Chọn đáp án D.
Câu 2: Chọn câu đúng:
A. Qua hai điểm phân biệt có vô số đường thẳng.
B. Có vô số điểm thuộc một đường thẳng.
C. Hai đường thẳng phân biệt thì song song.
D. Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.
Đáp án
• Đáp án A: Qua hai điểm phân biệt có một và chỉ một đường thẳng nên A sai.
• Đáp án B: Có vô số điểm thuộc một đường thẳng nên B đúng.
• Đáp án C: Hai đường thẳng phân biệt thì có thể song song hoặc cắt nhau nên C sai.
• Đáp án D: Trong ba điểm thẳng hàng thì chỉ có một điểm nằm giữa hai điểm còn lại nên D sai.
Chọn đáp án B.
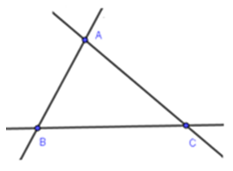
Câu 3: Cho ba điểm A; B; C không thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được những đường thẳng nào?
A. AB, BC, CA B. AB, BC, CA, BA, CB, AC
C. AA, BC, CA, AB D. AB, BC, CA, AA, BB, CC
Đáp án
Các đường thẳng trong hình là: AB, BC, CA
Chọn đáp án A.
Câu 4: Cho 5 điểm A; B; C; D; E trong đó không có ba điểm nào thẳng hàng. Vẽ đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng?
A. 25 B. 10 C. 20 D. 16
Đáp án
Các đường thẳng là: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE
Vậy có tất cả 10 đường thẳng cần tìm.
Chọn đáp án B.
Câu 5: Cho 3 đường thẳng a, b, c phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
A. Ba đường thẳng đôi một cắt nhau. B. a cắt b và a song song c.
C. Ba đường thẳng đôi một song song. D. a song song b và a cắt c.
Đáp án
Ba đường thẳng đôi một không có giao điểm nghĩa là:
• a, b không có giao điểm hay a song song b.
• b, c không có giao điểm hay b song song c.
• a, c không có giao điểm hay a song song c.
Vậy ba đường thẳng đôi một song song.
Chọn đáp án C.
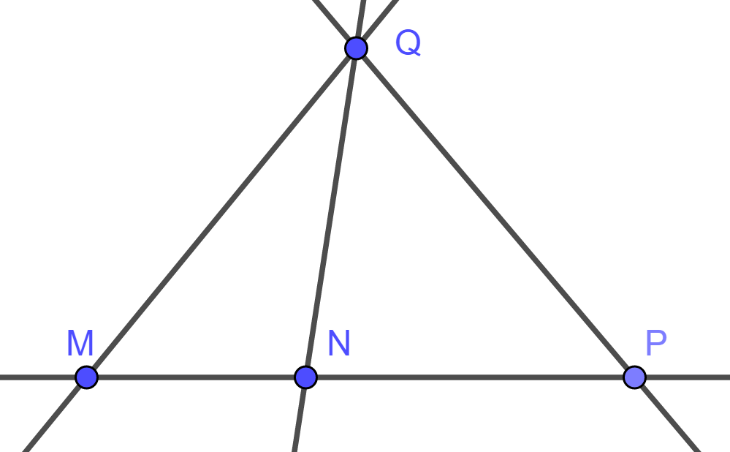
Câu 6: Cho bốn điểm M, N, P ,Q trong đó ba điểm M, N, P thẳng hàng và điểm Q nằm ngoài đường thẳng trên. Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng phân biệt?
A. 3
B. 4
C. 5
D. 6
Đáp án
Vì ba điểm M, N, P thẳng hàng nên qua hai điểm bất kì trong ba điểm trên ta đều nhận được một đường thẳng. Vậy từ ba điểm trên ta được một đường thẳng.
Các đường thẳng còn lại là: QM, QN, QP
Vậy có tất cả 4 đường thẳng phân biệt
Chọn đáp án B
Câu 7: Cho ba điểm A, B, C không thẳng hàng. Ta nói gì về hai đường thẳng AB và AC
A. Trùng nhau
B. Song song
C. Cắt nhau
D. Đáp án khác
Đáp án
Vì A, B, C không thẳng hàng nên AB và AC phân biệt
Mà AB và AC có điểm chung duy nhất là A nên hai đường thẳng AB và AC cắt nhau
Chọn đáp án C
Câu 8: Trong các khẳng định sau, khẳng định đúng là:
A. Có một và chỉ một đường thẳng đi qua hai điểm ( phân biệt) cho trước
B. Có đúng ba đường thẳng đi qua ba điểm ( phân biệt) cho trước
C. Có đúng sáu đường thẳng đi qua bốn điểm ( phân biệt) cho trước
D. Ba đường thẳng phân biệt, đôi một cắt nhau thì có đúng 3 giao điểm ( phân biệt)
Đáp án
Có một và chỉ một đường thẳng đi qua hai điểm ( phân biệt) cho trước Đáp án A đúng
Ba điểm phân biệt có thể thẳng hàng hoặc không. Trong trường hợp ba điểm phân biệt thẳng hàng thì ta chỉ xác định được duy nhất một đường thẳng đi qua ba điểm phân biệt đó. Do đó, đáp án B sai
Tương tự, nếu bốn điểm phân biệt đó không thẳng hàng thì ta mới xác định được sáu đường thẳng đi qua bốn điểm phân biệt đó. Nếu trong bốn điểm phân biệt đó, có ba điểm thẳng hàng ta chỉ xác định được 4 đường thẳng, hoặc cả 4 điểm phân biệt đó đều thẳng hàng ta chỉ xác định được 1 đường thẳng. Do đó, đáp án C sai
Ba đường thẳng phân biệt có thể song song hoặc cắt nhau. Nếu ba đường thẳng đó đôi một cắt nhau thì ta có ba giao điểm. Nếu trong ba đường thẳng phân biệt đó, có hai đường thẳng song song với nhau, đường thẳng thứ ba cắt 2 đường thẳng còn lại thì ta có 2 giao điểm. Vậy đáp án D sai
Chọn đáp án A
Câu 9: Cho năm đường thẳng cắt nhau từng đôi một cho ít nhất mấy giao điểm
A. 1
B. 2
C. 3
D. 4
Đáp án
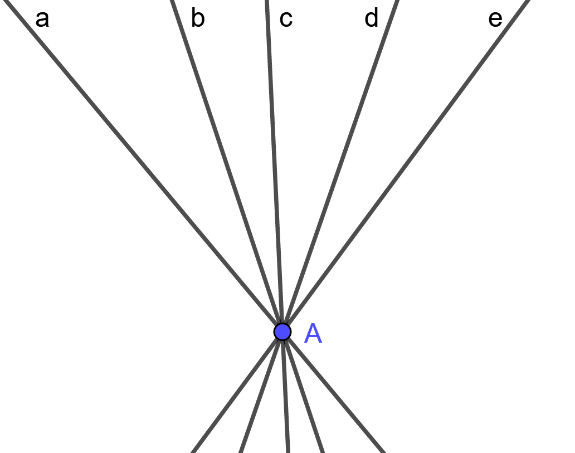
Cho 5 đường thẳng cắt nhau từng đôi một, trường hợp cho ít giao điểm nhất là cả năm đường thẳng đều đi qua một điểm
5 đường thẳng a, b, c, d, e cắt nhau tại điểm A
Chọn đáp án A
Câu 10: Cho ba đường thẳng cắt nhau từng đôi một cho nhiều nhất mấy giao điểm
A. 1
B. 2
C. 3
D. 4
Đáp án
Ba đường thẳng cắt nhau từng đôi một cho ta nhiều nhất ba giao điểm
Chọn đáp án C