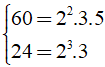Bài 18: Bội chung nhỏ nhất

A. Lý thuyết

1. Định nghĩa: Bội chung nhỏ nhất (BCNN) của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Ví dụ:

B(4) = {0; 4; 8; 12; 16; 20; 24; ...}

B(6) = {0; 6; 12; 18; 24; ...}

⇒ BC(4; 6) = {0; 12; 24; ...}

⇒ BCNN(4; 6) = 12

Chú ý: Mọi số tự nhiên đều là bội của 1. Do đó: Với mọi số tự nhiên a và b ( khác 0) ta có:

BCNN(a; 1) = a; BCNN(a,b,1) = BCNN(a,b)

Ví dụ:

BCNN(6;1) = 6

BCNN(6;8;1) = BCNN(6;8)

2. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:

   + Phân tích mỗi số ra thừa số nguyên tố.

   + Chọn ra các thừa tố nguyên tố chung và riêng.

   + Lập tích các thừa số đã chọn, mỗi thừa số lấy số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ví dụ: Tìm BCNN(8;12)

Ta có:

8 = 2³

12 = 2³

Chọn ra các thừa số chung và riêng, đó là 2 và 3. Số mũ lớn nhất của 2 là 3, số mũ lớn nhất của 3 là 1. Khi đó:

BCNN(8; 12) = 2³.3 = 24

Chú ý:

   • Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó

Ví dụ: BCNN(3; 5; 7) = 3.5.7 = 105

   • Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.

Ví dụ: BCNN(12;16;48) = 48

3. Cách tìm bội chung thông qua tìm BCNN

Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó

Ví dụ: Tìm bội chung của 8 và 12

Ta đã chỉ ra ở VD trên: BCNN(8; 12) = 24

⇒ BC(8; 12) = B(24) = {0; 24; 48; 72;...}

4. Bài tập tự luyện

Câu 1: Tìm BCNN(38; 76)?

A. 2888     B. 37     C. 76     D. 144

Hướng dẫn giải:

Ta có 76 ⋮ 38 ⇒ BCNN(38, 76) = 76

Chọn đáp án C.

Câu 2: Một khu đất hình chữ nhất có chiều dài là 60cm, chiều rộng là 24cm. Người ta chia thành những thửa đất hình vuông bằng nhau, để mỗi thửa đất có diện tích lớn nhất thì độ dài mỗi cạnh của thửa đất đó bằng?

Hướng dẫn giải:

Gọi độ dài cạnh của mỗi thửa đất hình vuông là x (cm)

Để diện tích của một thửa đất đó lớn nhất thì độ dài x lớn nhất.

Vì các thửa đất đó được chia ra từ khu đất hình chữ nhật có chiều dài là 60cm, chiều rộng là 24cm

Nên x phải là ước của 60 và 24 hay x ∈ ƯC(24; 60)

Khi đó x lớn nhất thì x = ƯCLN(24; 60)

Ta có: 

⇒ ƯCL(24; 60) = 2².3 = 12

Vậy mỗi thừa đất hình vuông có độ dài cạnh lớn nhất là 12cm

B. Bài tập trắc nghiệm

Câu 1: BCNN (86; 108) là:

A. 12

B. 108

C. 60

D. 540

Đáp án

Câu 2: BCNN (40; 28; 140) là:

A. 140

B. 280

C. 420

D. 560

Đáp án

Câu 3: Số tự nhiên a nhỏ nhất khác 0 thỏa mãn a ⋮ 18 và a ⋮ 40

A. 360

B. 400

C. 458

D. 500

Đáp án

Câu 4: BCNN (12; 18; 108) là:

A. 0

B. 108

C. 144

D. 216

Đáp án

Câu 5: Tìm số tự nhiên x biết rằng : x ⋮ 12; x ⋮ 28; x ⋮ 36 và 150 < x < 300

A. x = 36

B. x = 108

C. x = 252

D. x = 288

Đáp án

Câu 6: Học sinh lớp 6D khi xếp hàng 2, hàng 3, hàng 6, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng từ 40 đến 60. Số học sinh của lớp 6D là:

A. 48

B. 54

C. 60

D. 72

Đáp án

Câu 7: Trong các khẳng định sau, khẳng định nào đúng?

A. BCNN của a và b là số nhỏ nhất trong tập hợp bội chung của a và b

B. BCNN(a, b, 1) = BCNN(a, b)

C. Nếu m ⋮ n thì BCNN (m; n) = n

D. Nếu UCLN(x; y) = 1 thì BCNN(x; y) = 1

Đáp án

Câu 8: Tìm số tự nhiên nhỏ nhất có ba chữ số, biết rằng số đó chia hết cho 3; 4; 5

A. 102

B. 120

C. 135

D. 150

Đáp án

Câu 9: Hai bạn Tít và Mít thường đến thư viện đọc sách. Tít cứ 9 ngày đến thư viện một lần, Mít 12 ngày một lần. Lần đầu cả hai bạn cùng đến thư viện vào một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn lại đến cùng thư viện?

A. 24

B. 27

C. 36

D. 42

Đáp án

Câu 10: BCNN (5; 7; 17) là:

A. 595

B. 714

C. 833

D. 1190

Đáp án