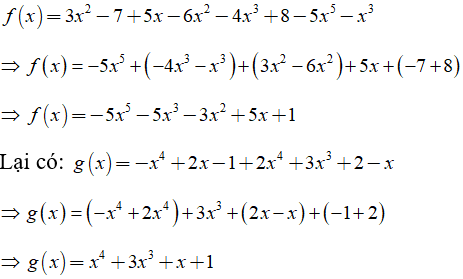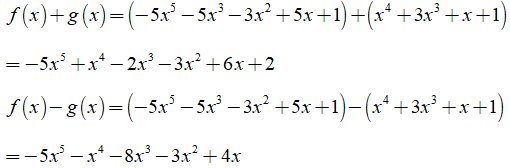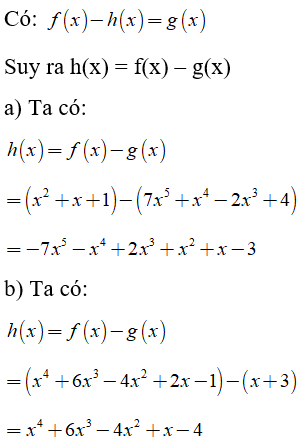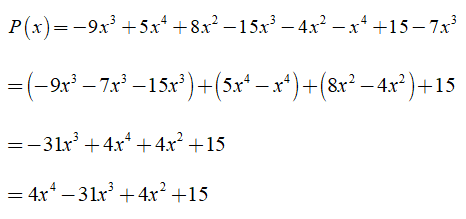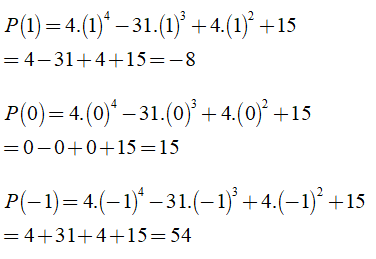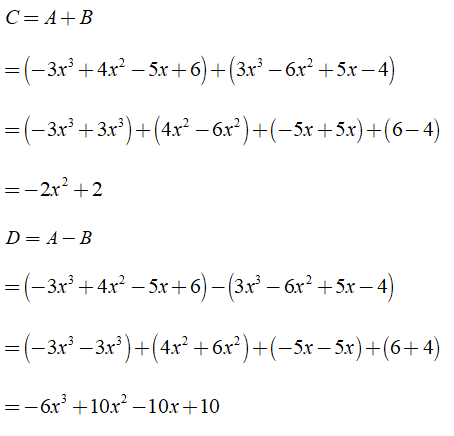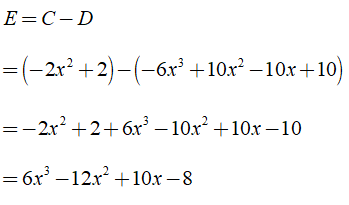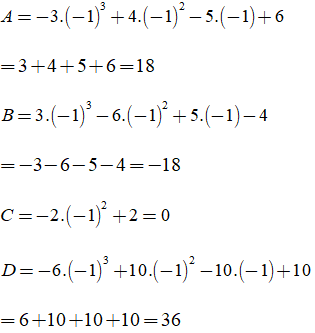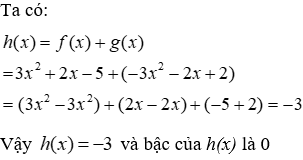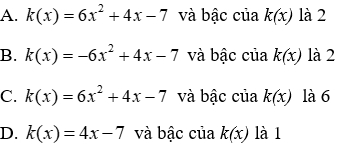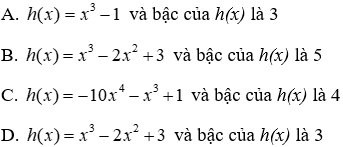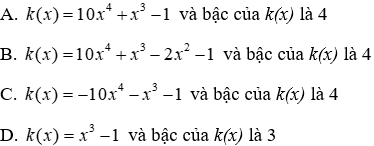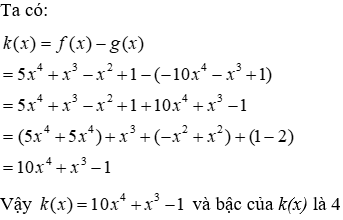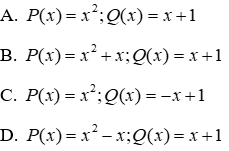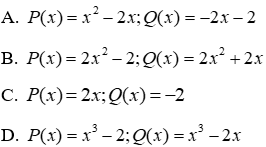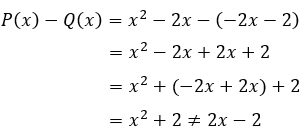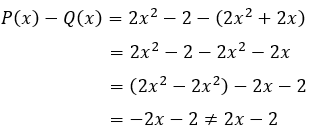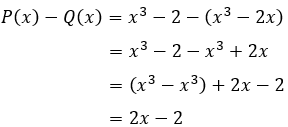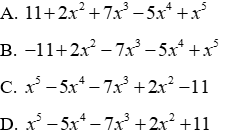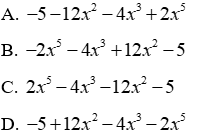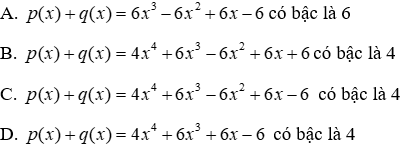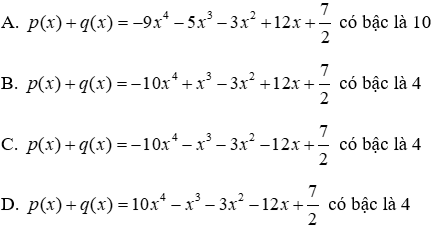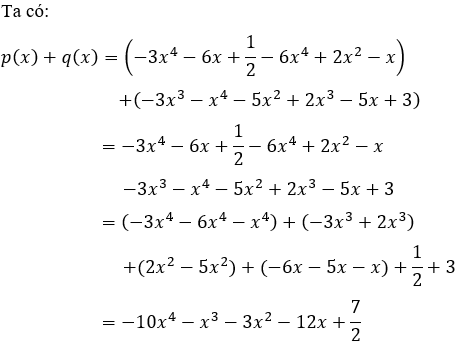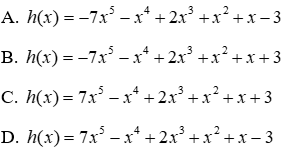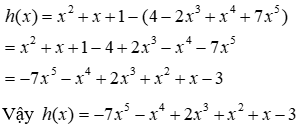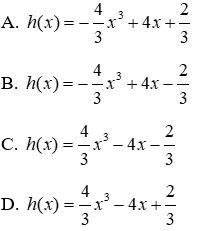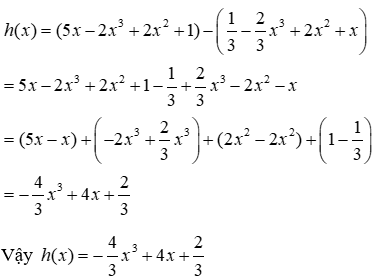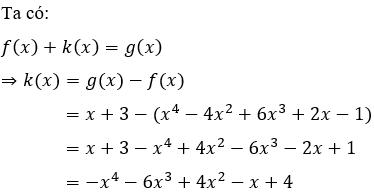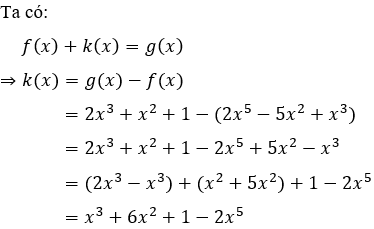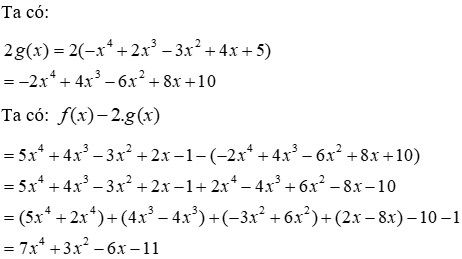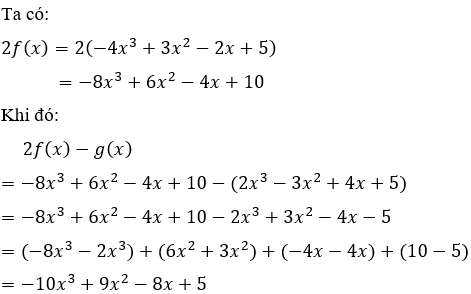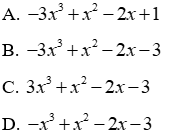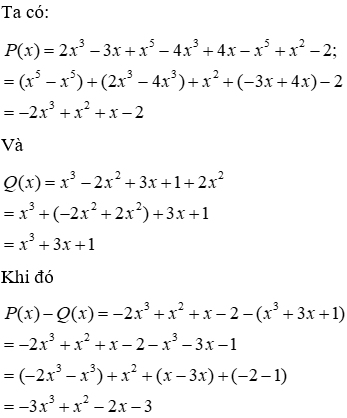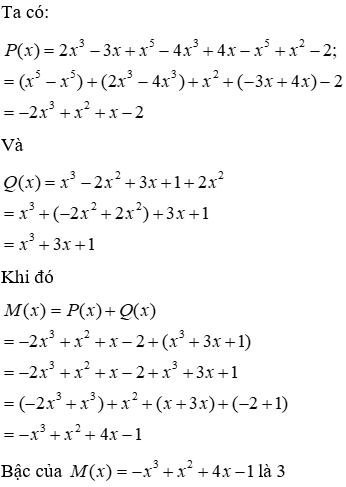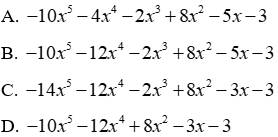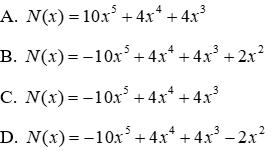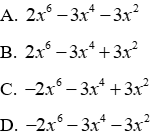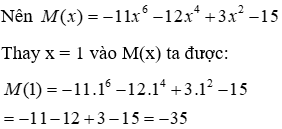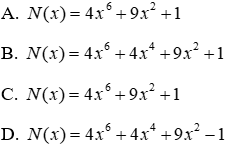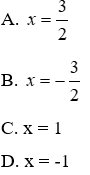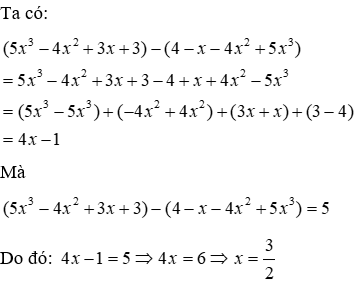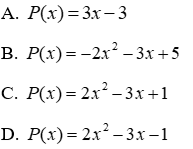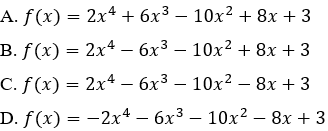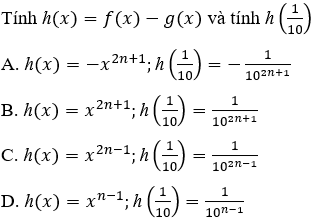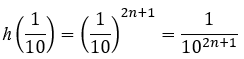Toán học 7 Bài 48: Cộng, trừ đa thức một biến
Lý thuyết tổng hợp Toán học lớp 7 Bài 48: Cộng, trừ đa thức một biến, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 48: Cộng, trừ đa thức một biến
A. Lý thuyết
Để cộng (hay trừ) các đa thức một biến, ta làm một trong hai cách sau:
• Cách 1: Cộng, trừ đa thức theo “hàng ngang”
• Cách 2: Sắp xếp các hạng từ của hai đa thức cùng theo lũy thừa giảm (hoặc tăng) của biến rồi đặt phép tính theo cột dọc tương ứng như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng ở cùng một cột)
Ví dụ 1: Cho hai đa thức P(x) = x5 - 2x4 + x2 - x + 1; Q(x) = 6 - 2x + 3x3 + x4 - 3x5. Tính P(x) - Q(x).
P(x) - Q(x) = (x5 - 2x4 + x2 - x + 1) - (6 - 2x + 3x3 + x4 - 3x5)
= x5 - 2x4 + x2 - x + 1 - 6 + 2x - 3x3 - x4 + 3x5
= (x5 + 3x5) + (-2x4 - x4) - 3x3 + x2 + (-x + 2x) + (1 - 6)
= 4x5 - 3x4 - 3x3 + x2 + x5
Ví dụ 2: Cho các đa thức
f(x) = 3x2 - 7 + 5x - 6x2 - 4x3 + 8 - 5x5 - x3
g(x) = -x4 + 2x - 1 + 2x4 + 3x3 + 2 - x
a) Thu gọn các đa thức trên rồi sắp xếp chúng theo thứ tự giảm dần lũy thừa của biến
b) Xác định bậc của mỗi đa thức
c) Cho biết hệ số cao nhất và hệ số tự do của mỗi đa thức
d) Tính f(x) + g(x) và f(x) - g(x)
Hướng dẫn giải:
a) Ta có
b) Đa thức f(x) có bậc 5
Đa thức g(x) có bậc 4
c) Đa thức f(x) có hệ số cao nhất là -5 và hệ số tự do là 1
Đa thức g(x) có hệ số cao nhất là 1 và hệ số tự do là 1
d) Ta có:
Ví dụ 3: Tìm đa thức h(x) sao cho f(x) - h(x) = g(x) biết
a) f(x) = x2 + x + 1 và g(x) = 7x5 + x4 - 2x3 + 4
b) f(x) = x4 + 6x3 - 4x2 + 2x - 1 và g(x) = x + 3
Hướng dẫn giải:
Bài tập vận dụng
Bài 1: Cho đa thức P(x) = -9x3 + 5x4 + 8x2 - 15x3 - 4x2 - x4 + 15 - 7x3
Tính P(1), P(0), P(-1)
Hướng dẫn giải:
Trước hết ta thu gọn đa thức:
Khi đó ta có:
Bài 2: Cho đa thức
A = -3x3 + 4x2 - 5x + 6
B = 3x3 - 6x2 + 5x - 4
a) Tính C = A + B, D = A - B, E = C - D
b) Tính các giá trị của đa thức A, B, C, D tại x = -1
Hướng dẫn giải:
a) Ta có:
b) Tính giá trị biểu thức tại x = -1
B. Bài Tập
Câu 1: Cho hai đa thức f(x) = 3x2 + 2x - 5 và g(x) = -3x2 - 2x + 2
1.1: Tính h(x) = f(x) + g(x) và tìm bậc của h(x)
Lời giải:
Đáp án cần chọn là: D
1.2: Tính k(x) = f(x) - g(x) và tìm bậc của k(x)
Lời giải:
Đáp án cần chọn là: A
Câu 2: Cho hai đa thức f(x) = 5x4 + x3 - x2 + 1 và g(x) = -5x4 - x2 + 2
2.1: Tính h(x) = f(x) + g(x) và tìm bậc của h(x)
Lời giải:
Đáp án cần chọn là: D
2.2: Tính k(x) = f(x) - g(x) và tìm bậc của k(x)
Lời giải:
Đáp án cần chọn là: A
Câu 3: Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) + Q(x) = x2 + 1
Lời giải:
Đáp án cần chọn là: D
Câu 4: Cho hai đa thức P(x) và Q(x) dưới đây, hai đa thức nào thỏa mãn P(x) - Q(x) = 2x - 2
Lời giải:
Theo đề bài ta có: P(x) - Q(x) = 2x - 2
Thử đáp án A với P(x) = x2 - 2x; Q(x) = -2x - 2 thì
Do đó đáp án A không thỏa mãn yêu cầu bài toán
Thử đáp án B với P(x) = 2x2 - 2; Q(x) = 2x2 + 2x thì
Do đó đáp án B không thỏa mãn yêu cầu bài toán
Thử đáp án C với P(x) = 2x; Q(x) = -2 thì
P(x) - Q(x) = 2x-(-2) = 2x + 2 ≠ 2x - 2
Do đó đáp án C không thỏa mãn yêu cầu bài toán
Thử đáp án D với P(x) = x3 - 2; Q(x) = x3 - 2x thì
Do đó đáp án D thỏa mãn yêu cầu bài toán
Đáp án cần chọn là: D
Câu 5: Cho f(x) = x5 - 3x4 + x2 - 5 và g(x) = 2x4 + 7x3 - x2 + 6. Tính hiệu f(x) - g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
Lời giải:
Ta có:
f(x) - g(x) = x5 - 3x4 + x2 - 5-(2x4 + 7x3 - x2 + 6)
= x5 - 3x4 + x2 - 5 - 2x4 - 7x3 + x2 - 6
= x5 + (-3x4 - 2x4)-7x3 + (x2 + x2)-5-6
= x5 - 5x4 - 7x3 + 2x2 - 11
Sắp xếp kết quả theo lũy thừa tăng dần của biến ta được: -11 + 2x2 - 7x3 - 5x4 + x5
Đáp án cần chọn là: B
Câu 6: Cho f(x) = 5x4 - 4x3 + 6x2 - 2x + 1 và g(x) = 2x5 + 5x4 - 6x2 - 2x+6. Tính hiệu f(x) - g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
Lời giải:
Ta có:
f(x) - g(x) = 5x4 - 4x3 + 6x2 - 2x + 1-(2x5 + 5x4 - 6x2 - 2x+6)
= 5x4 - 4x3 + 6x2 - 2x + 1 - 2x5 - 5x4 + 6x2 + 2x - 6
= (5x4 - 5x4) - 4x3 + (6x2 + 6x2) + (-2x + 2x) - 2x5 + 1-6
= - 4x3 + 12x2 - 5 - 2x5
Sắp xếp kết quả theo lũy thừa tăng dần của biến ta được: -5 + 12x2 - 4x3 - 2x5
Đáp án cần chọn là: D
Câu 7: Cho P(x) = 5x4 + 4x3 - 3x2 + 2x - 1 và Q(x) = -x4 + 2x3 - 3x2 + 4x - 5. Tính P(x) + q(x) rồi tìm bậc của đa thức thu gọn
Lời giải:
Ta có:
P(x) + Q(x) = 5x4 + 4x3 - 3x2 + 2x - 1 + (-x4 + 2x3 - 3x2 + 4x - 5)
= 5x4 + 4x3 - 3x2 + 2x - 1-x4 + 2x3 - 3x2 + 4x - 5
= (5x4 - x4) + (4x3 + 2x3) + (-3x2 - 3x2) + (2x + 4x)-1-5
= 4x4 + 6x3 - 6x2 + 6x - 6
Bậc của đa thức P(x) + Q(x) = 4x4 + 6x3 - 6x2 + 6x - 6 là 4
Đáp án cần chọn là: C
Câu 8: Cho 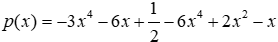
Lời giải:
Bậc của đa thức 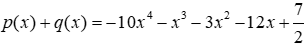
Đáp án cần chọn là: C
Câu 9: Tìm đa thức h(x) biết f(x) - h(x) = g(x) và f(x) = x2 + x + 1; g(x) = 4 - 2x3 + x4 + 7x5
Lời giải:
Ta có: f(x) - h(x) = g(x) ⇒ h(x) = f(x) - g(x)
Mà f(x) = x2 + x + 1; g(x) = 4 - 2x3 + x4 + 7x5 nên
Đáp án cần chọn là: A
Câu 10: Tìm đa thức h(x) biết f(x) - h(x) = g(x) và
Lời giải:
Ta có: f(x) - h(x) = g(x) ⇒ h(x) = f(x) - g(x)
Mà 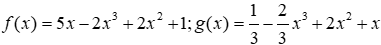
Đáp án cần chọn là: A
Câu 11: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = x4 - 4x2 + 6x3 + 2x - 1; g(x) = x + 3
A. -1
B. 1
C. 4
D. 6
Lời giải:
Nhận thấy số hạng có lũy thừa cao nhất của biến -x4 nên hệ số cao nhất là -1
Đáp án cần chọn là: A
Câu 12: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = 2x5 - 5x2 + x3; g(x) = 2x3 + x2 + 1
A. -1
B. 1
C. -2
D. 6
Lời giải:
Sắp xếp các hạng tử của đa thức k(x) theo lũy thừa giảm dần của biến x ta được k(x) = x3 + 6x2 + 1 - 2x5
Hệ số cao nhất của k(x) là -2
Đáp án cần chọn là: C
Câu 13:Tìm hệ số tự do của hiệu f(x)-2.g(x) với f(x) = 5x4 + 4x3 - 3x2 + 2x - 1; g(x) = -x4 + 2x3 - 3x2 + 4x+5
A. 7
B. 11
C. -11
D. 4
Lời giải:
Hệ số tự do cần tìm là -11
Đáp án cần chọn là: C
Câu 14: Tìm hệ số tự do của hiệu 2f(x) - g(x) với f(x) = - 4x3 + 3x2 - 2x+5; g(x) = 2x3 - 3x2 + 4x+5
A. 10
B. -5
C. 5
D. -8
Lời giải:
Hệ số tự do cần tìm là 5
Đáp án cần chọn là: C
Câu 15: Cho hai đa thức P(x) = 2x3 - 3x + x5 - 4x3 + 4x - x5 + x2 - 2; và Q(x) = x3 - 2x2 + 3x + 1 + 2x2
15.1: Tính P(x) - Q(x)
Lời giải:
Đáp án cần chọn là: B
15.2: Tìm bậc của đa thức M(x) = P(x) + Q(x)
A. 4
B. 2
C. 3
D. 1
Lời giải:
Đáp án cần chọn là: C
Câu 16: Cho hai đa thức P(x) = -6x5 - 4x4 + 3x2 - 2x; và Q(x) = 2x5 - 4x4 - 2x3 + 2x2 - x - 3
16.1: Tính 2P(x) + Q(x)
Lời giải:
Đáp án cần chọn là: B
16.2: Gọi M(x) = P(x) - Q(x). Tính M(-1)
A. 11
B. -10
C. -11
D. 10
Lời giải:
Ta có: M(x) = P(x) - Q(x)
M(x) = P(x) - Q(x)
= -6x5 - 4x4 + 3x2 - 2x-(2x5 - 4x4 - 2x3 + 2x2 - x - 3)
= -6x5 - 4x4 + 3x2 - 2x - 2x5 + 4x4 + 2x3 - 2x2 + x + 3
= (-6x5 - 2x5) + ( - 4x4 + 4x4) + 2x3 + (3x2 - 2x2) + (-2x + x) + 3
= -8x5 + 2x3 + x2 - x + 3
Nên M(x) = -8x5 + 2x3 + x2 - x + 3
Thay x = -1 vào M(x) ta được
M(-1) = -8.(-1)5 + 2.(-1)3 + (-1)2 - (-1) + 3
= 8 - 2 + 1 + 1 + 3 = 11
Đáp án cần chọn là: A
16.3: Tìm N(x) biết P(x) - 2Q(x) = N(x)-x2 + 6
Lời giải:
Ta có:
2Q(x) = 2(2x5 - 4x4 - 2x3 + 2x2 - x - 3)
= 4x5 - 8x4 - 4x3 + 4x2 - 2x - 6
Khi đó
P(x) - 2Q(x)
= -6x5 - 4x4 + 3x2 - 2x-(4x5 - 8x4 - 4x3 + 4x2 - 2x - 6)
= -6x5 - 4x4 + 3x2 - 2x - 4x5 + 8x4 + 4x3 - 4x2 + 2x+6
= (-6x5 - 4x5) + ( - 4x4 + 8x4)+4x3 + (3x2 - 4x2) + (-2x + 2x)+6
= -10x5 + 4x4 + 4x3 - x2 + 6
Nên P(x) - 2Q(x) = N(x)-x2 + 6
⇒ N = P(x) - 2Q(x) - (-x2 + 6)
= -10x5 + 4x4 + 4x3 - x2 + 6-(-x2 + 6)
= -10x5 + 4x4 + 4x3 - x2 + 6 + x2 - 6
= -10x5 + 4x4 + 4x3
Nên N(x) = -10x5 + 4x4 + 4x3
Đáp án cần chọn là: C
Câu 17: Cho hai đa thức P(x) = -3x6 - 5x4 + 2x2 - 5; Q(x) = 8x6 + 7x4 - x2 + 10
17.1: Tính 2P(x) + Q(x)
Lời giải:
Ta có:
2P(x) = 2(-3x6 - 5x4 + 2x2 - 5)
= -6x6 - 10x4 + 4x2 - 10
Khi đó:
2P(x) + Q(x)
= -6x6 - 10x4 + 4x2 - 10 + 8x6 + 7x4 - x2 + 10
= (-6x6 + 8x6) + (-10x4 + 7x4) + (4x2 - x2) + (-10+10)
= 2x6 - 3x4 + 3x2
Đáp án cần chọn là: B
17.2: Gọi M(x) = P(x) - Q(x). Tính M(1)
A. -35
B. -3
C. 35
D. 3
Lời giải:
Ta có: M(x) = P(x) - Q(x)
= -3x6 - 5x4 + 2x2 - 5-(8x6 + 7x4 - x2 + 10)
= -3x6 - 5x4 + 2x2 - 5-8x6 - 7x4 + x2 - 10
= (-3x6 - 8x6) + (-5x4 - 7x4) + (2x2 + x2) + (-10-5)
= -11x6 - 12x4 + 3x2 - 15
Đáp án cần chọn là: A
17.3: Tìm N(x) biết P(x) + Q(x) = N(x)+C(x) với C(x) = x6 + 2x4 - 8x2 + 6
Lời giải:
Ta có: P(x) + Q(x)
= -3x6 - 5x4 + 2x2 - 5 + 8x6 + 7x4 - x2 + 10
= (-3x6 + 8x6) + (-5x4 + 7x4) + (2x2 - x2) + (-5+10)
= 5x6 + 2x4 + x2 + 5
Theo đề bài ra ra có:
P(x) + Q(x) = N(x)+C(x)
⇒ N(x) = [P(x) + Q(x)]-C(x)
⇒ N(x) = 5x6 + 2x4 + x2 + 5-(x6 + 2x4 - 8x2 + 6)
= 5x6 + 2x4 + x2 + 5-x6 - 2x4 + 8x2 - 6
= (5x6 - x6) + (2x4 - 2x4) + (x2 + 8x2) + (5-6)
= 4x6 + 9x2 - 1
Đáp án cần chọn là: C
Câu 18: Tìm x biết (5x3 - 4x2 + 3x + 3) - (4-x - 4x2 + 5x3) = 5
Lời giải:
Đáp án cần chọn là: A
Câu 19: Xác định P(x) = ax2 + bx + c biết P(1) = 0;P(-1) = 6;P(2) = 3
Lời giải:
Thay x = 1 vào P(x) = a x 2 + bx + c ta được:
P(1) = a. 1 2 + b.1 + c = A + B + C
Mà P(1) = 0 suy ra A + B + C hay a + c = -b (1)
Thay x = -1 vào P(x) = a x 2 + bx + c ta được:
P(-1) = a.(-1)2 + b.(-1) + c = a - b + C
Mà P (-1) = 6 suy ra a-B + C =6 hay a + c = 6 + b (2)
Thay x = 2 vào P(x) = a x 2 + bx + c ta được:
P(2) = a. 22 + b.2 + c = 4a + 2B + C
Mà P(2) = 3 suy ra 4a + 2B + C = 3(3)
Từ (1),(2) ta có -b = 6 + b ⇒ -2b = 6 ⇒ b = -3
Thay b = -3 vào (1) ta được: a + c = 3 ⇒ c = 3-a (4)
Thay b = -3 vào (3) ta được (5)
Từ (4),(5) ta có:
3-a = 9-4a ⇒ -a + 4a = 9-3 ⇒ 3a = 6 ⇒ a = 2
Thay a = 2 vào (4) ta được c = 3 - 2 = 1
Vậy P(x) = 2x2 - 3x + 1
Đáp án cần chọn là: C
Câu 20: Tìm f(x) biết f(x) + g(x) = 6x4 - 3x2 - 5 và g(x) = 4x4 - 6x3 + 7x2 + 8x-8
Lời giải:
Ta có:
f(x) + g(x) = 6x4 - 3x2 - 5 ⇒ f(x) = (6x4 - 3x2 - 5) - g(x)
⇒ f(x) = 6x4 - 3x2 - 5-(4x4 - 6x3 + 7x2 + 8x - 8)
= 6x4 - 3x2 - 5 - 4x4 + 6x3 - 7x2 - 8x + 8
= (6x4 - 4x4)+6x3 + (-3x2 - 7x2)-8x + (-5 + 8)
= 2x4 + 6x3 - 10x2 - 8x + 3
Đáp án cần chọn là: A
Câu 21: Cho f(x) = x2n - x2n-1 + ... + x2 - x + 1; g(x) = -x2n+1 + x2n - x2n-1 + ... + x2 - x + 1
Lời giải:
Ta có:
h(x) = f(x) - g(x)
= (x2n - x2n-1 + ... + x2 - x + 1) - (-x2n+1 + x2n - x2n-1 + ... + x2 - x + 1)
= x2n - x2n-1 + ... + x2 - x + 1 + x2n+1 - x2n + x2n-1 - ...-x2 + x-1
= x2n+1 + (x2n - x2n) + (-x2n-1 + x2n-1) + ... . + (x2 - x2) + (-x + x) + (1-1)
= x2n+1
Thay 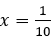
Đáp án cần chọn là: B