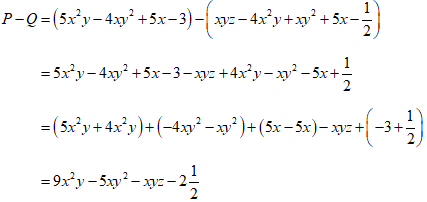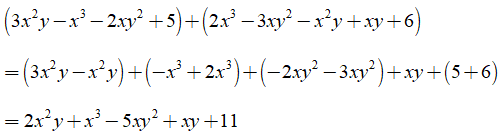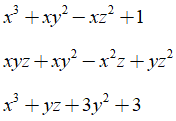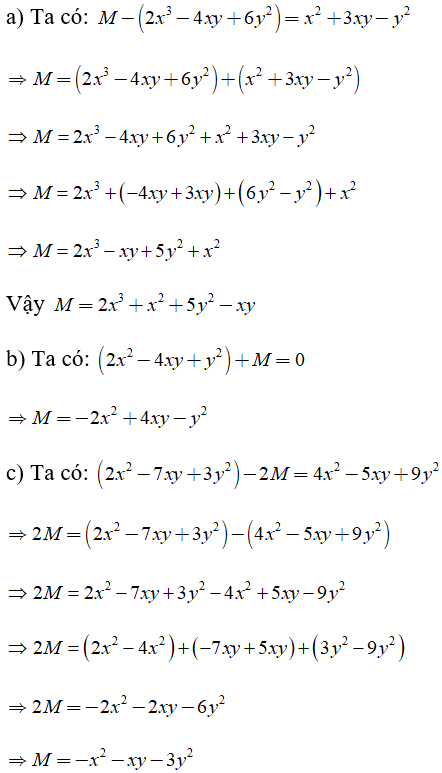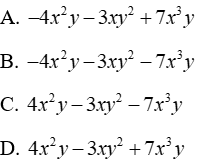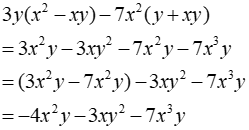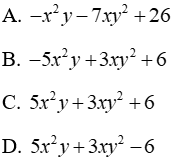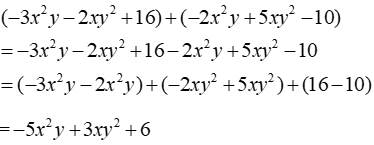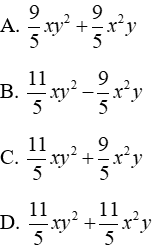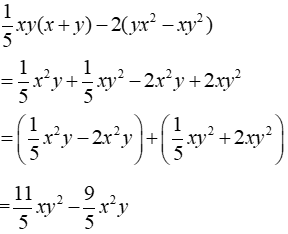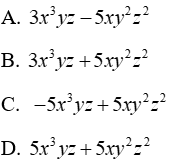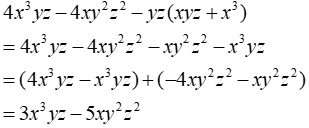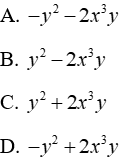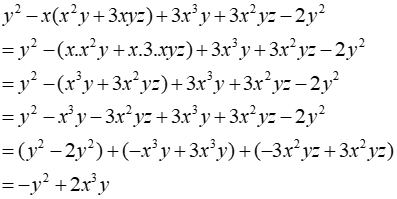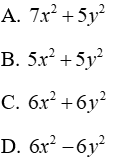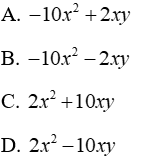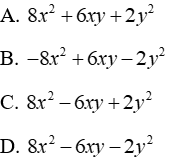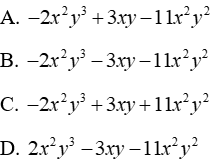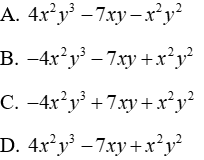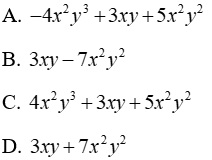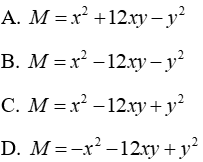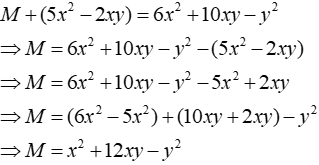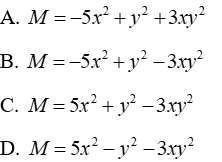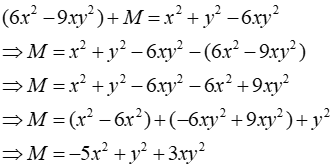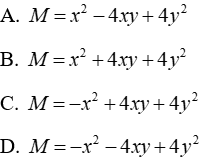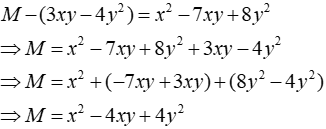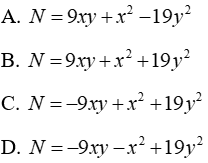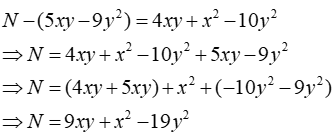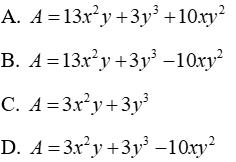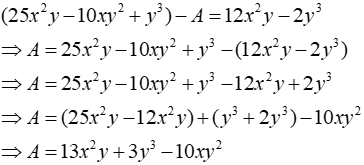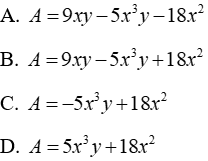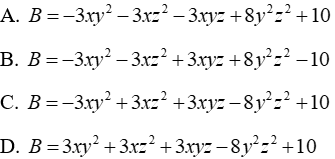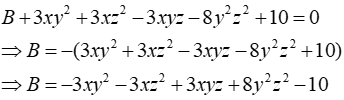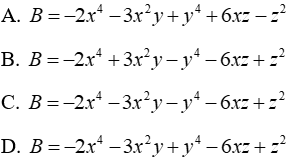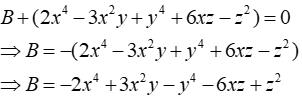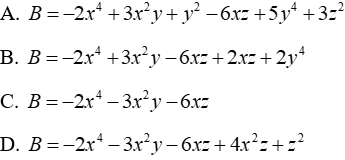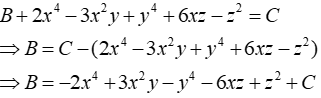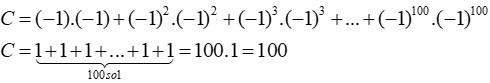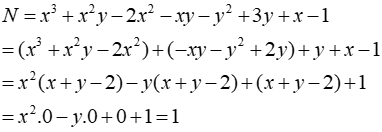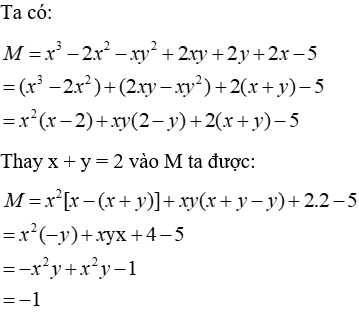Toán học 7 Bài 46: Cộng, trừ đa thức
Lý thuyết tổng hợp Toán học lớp 7 Bài 46: Cộng, trừ đa thức, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 46: Cộng, trừ đa thức
A. Lý thuyết
Để cộng (hay trừ) hai đa thức, ta làm như sau:
• Bước 1: Viết hai đa thức trong dấu ngoặc.
• Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc).
• Bước 3: Nhóm các hạng tử đồng dạng.
• Bước 4: Cộng, trừ các đơn thức đồng dạng.
Ví dụ 1: Cộng hai đa thức M = 5x2y + 5x + 3 và N = xyz - 4x2y + 5x - 1/2
Ta có:
Ví dụ 2: Trừ hai đa thức P = 5x2y - 4xy2 + 5x - 3 và Q = xyz - 4x2y + xy2 + 5x - 1/2
Ta có:
Ví dụ 3: Tính tổng của 3x2y - x3 - 2xy2 + 5 và 2x3 - 3xy2 - x2y + xy + 6
Hướng dẫn giải:
Tổng của hai đa thức là:
Ví dụ 4: Viết một đa thức bậc 3 có chứa ba biến và có bốn hạng tử
Hướng dẫn giải:
Có nhiều cách viết chẳng hạn như:
Bài tập vận dụng
Bài 1: Tìm đa thức M biết
a) M - (2x3 - 4xy + 6y2) = x2 + 3xy - y2
b) (2x2 - 4xy + y2) + M = 0
c) (2x2 -7xy + 3y2) - 2M = 4x2 - 5xy + 9y2
Hướng dẫn giải:
Bài 2: Tính giá trị của các đa thức sau
a) 2x3 + y2 + 2xy - 3y3 + 2x3 + 3y3 - 3x3 tại x = 4; y = 5
b) x6y6 - x4y4 + x2y - xy + 1 tại x = 1; y = -1
Hướng dẫn giải:
a) Ta có : 2x3 + y2 + 2xy - 3y3 + 2x3 + 3y3 - 3x3
= (2x3 + 2x3 - 3x3) + y2 + 2xy + (-3y3 + 3y3)
= x3 + y2 + 2xy
Tại x = 4, y = 5, ta có:
43 + 52 + 2.4.5 = 64 + 25 + 40 = 129
b) Ta có: x6y6 - x4y4 + x2y - xy + 1
Tại x = 1, y = -1 ta có:
(1)6.(-1)6 - (1)4.(-1)4 + (1)2.(-1) - 1.(-1) + 1 = 1 - 1 - 1 + 1 + 1 = 1
B. Bài Tập
Câu 1: Thu gọn đa thức 3y(x2 - xy) - 7x2 (y + xy) ta được
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 2: Thu gọn đa thức (-3x2y - 2xy2 + 16) + ( - 2x2y + 5xy2 - 10) ta được
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 3: Đa thức 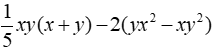
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 4: Đa thức (1,6x2 + 1,7y2 + 2xy) - (0,5x2 - 0,3y2 - 2xy) có bậc là
A. 2
B. 3
C. 4
D. 6
Lời giải:
Ta có:
(1,6x2 + 1,7y2 + 2xy) - (0,5x2 - 0,3y2 - 2xy)
= 1,6x2 + 1,7y2 + 2xy-0,5x2 + 0,3y2 + 2xy
= (1,6x2 - 0,5x2) + (1,7y2 + 0,3y2) + (2xy + 2xy)
= 1,1x2 + 2y2 + 4xy
Đa thức 1,1x2 + 2y2 + 4xy có bậc là 2
Đáp án cần chọn là: A
Câu 5: Đa thức nào dưới đây là kết quả của phép tính 4x3yz-4xy2 z2 - yz(xyz + x3)?
Lời giải:
Ta có:
Đáp án cần chọn là: A
Câu 6: Đa thức nào dưới đây là kết quả của phép tính y2 - x(x2y + 3xyz) + 3x3y + 3x2yz - 2y2?
Lời giải:
Ta có:
Đáp án cần chọn là: D
Câu 7: Cho các đa thức: A = 4x2 - 5xy + 3y2; B=3x2 + 2xy + y2; C = -x2 + 3xy + 2y2
7.1: Tính A + B + C
Lời giải:
Ta có:
A + B + C = 4x2 - 5xy + 3y2 + 3x2 + 2xy + y2 + (-x2 + 3xy + 2y2)
= 4x2 - 5xy + 3y2 + 3x2 + 2xy + y2 - x2 + 3xy + 2y2
= (4x2 + 3x2 - x2) + (-5xy + 2xy + 3xy) + (3y2 + y2 + 2y2)
= 6x2 + 6y2
Đáp án cần chọn là: C
7.2: Tính A - B - C
Lời giải:
Ta có:
A-B-C=4x2 - 5xy + 3y2 - (3x2 + 2xy + y2) - (-x2 + 3xy + 2y2)
= 4x2 - 5xy + 3y2 - 3x2 - 2xy - y2 + x2 - 3xy - 2y2
= (4x2 - 3x2 + x2) + (-5xy - 2xy - 3xy) + (3y2 - y2 - 2y2)
= 2x2 - 10xy
Đáp án cần chọn là: D
7.3: Tính C - A - B
Lời giải:
Ta có:
C-A-B=-x2 + 3xy + 2y2 - (4x2 - 5xy + 3y2) - (3x2 + 2xy + y2)
= -x2 + 3xy + 2y2 - 4x2 + 5xy - 3y2 - 3x2 - 2xy - y2
= (-x2 - 4x2 - 3x2) + (3xy + 5xy - 2xy) + (2y2 - 3y2 - y2)
= -8x2 + 6xy - 2y2
Đáp án cần chọn là: C
Câu 8: Cho các đa thức:
A = x2y3 - 2xy + 6x2y2;
B=3x2y2 - 2x2y3 + 2xy;
C=-x2y3 + 3xy + 2x2y2
8.1: Tính A + B + C
Lời giải:
Ta có:
A + B + C = x2y3 - 2xy + 6x2y2 + 3x2y2 - 2x2y3 + 2xy + (-x2y3 + 3xy + 2x2y2)
= x2y3 - 2xy + 6x2y2 + 3x2y2 - 2x2y3 + 2xy-x2y3 + 3xy + 2x2y2
= (x2y3 - 2x2y3 - x2y3) + (-2xy + 2xy + 3xy) + (6x2y2 + 3x2y2 + 2x2y2)
= - 2x2y3 + 3xy + 11x2y2
Đáp án cần chọn là: C
8.2: Tính A-B-C
Lời giải:
Ta có:
A-B-C=x2y3 - 2xy + 6x2y2 - (3x2y2 - 2x2y3 + 2xy) - (-x2y3 + 3xy + 2x2y2)
= x2y3 - 2xy + 6x2y2 - 3x2y2 + 2x2y3 - 2xy + x2y3 - 3xy - 2x2y2)
= (x2y3 + 2x2y3 + x2y3) + (-2xy - 2xy - 3xy) + (6x2y2 - 3x2y2 - 2x2y2)
= 4x2y3 - 7xy + x2y2
Đáp án cần chọn là: D
8.3: Tính C - A - B
Lời giải:
Ta có:
C - A - B =-x2y3 + 3xy + 2x2y2 - (x2y3 - 2xy + 6x2y2) - (3x2y2 - 2x2y3 + 2xy)
= -x2y3 + 3xy + 2x2y2 - x2y3 + 2xy-6x2y2 - 3x2y2 + 2x2y3 - 2xy
= (-x2y3 - x2y3 + 2x2y3) + (3xy + 2xy - 2xy) + (2x2y2 - 6x2y2 - 3x2y2)
= 3xy - 7x2y2
Đáp án cần chọn là: B
Câu 9: Tìm đa thức M biết M + (5x2 - 2xy) = 6x2 + 10xy - y2
Lời giải:
Ta có:
Đáp án cần chọn là: A
Câu 10: Tìm đa thức M biết (6x2 - 9xy2)+M=x2 + y2 - 6xy2
Lời giải:
Ta có:
Đáp án cần chọn là: A
Câu 11: Đa thức M nào dưới đây thỏa mãn M-(3xy-4y2) = x2 - 7xy+8y2
Lời giải:
Ta có:
Đáp án cần chọn là: A
Câu 12: Đa thức N nào dưới đây thỏa mãn N-(5xy - 9y2) = 4xy + x2 - 10y2
Lời giải:
Ta có:
Đáp án cần chọn là: A
Câu 13: Cho (25x2y - 10xy2 + y3)-A = 12x2y - 2y3. Đa thức A là:
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 14: Cho (19xy - 7x3y + 9x2)-A = 10xy - 2x3y - 9x2. Đa thức A là:
Lời giải:
Ta có:
(19xy - 7x3y + 9x2)-A = 10xy - 2x3y - 9x2
⇒ A = 19xy - 7x3y + 9x2 - 10xy + 2x3y + 9x2
⇒ A = (19xy - 10xy) + (-7x3y + 2x3y) + (9x2 + 9x2)
⇒ A = 9xy-5x3y + 18x2
Đáp án cần chọn là: B
Câu 15: Tìm đa thức B sao cho tổng B với đa thức 3xy2 + 3xz2 - 3xyz-8y2 z2 + 10 là đa thức 0
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 16: Tìm đa thức B sao cho tổng B với đa thức 2x4 - 3x2y + y4 + 6xz-z2 là đa thức 0
Lời giải:
Ta có:
Đáp án cần chọn là: B
Câu 17: Đa thức B nào dưới đây thỏa mãn tổng của B với đa thức 2x4 - 3x2y + y4 + 6xz-z2 là đa thức không chứa biến x
Lời giải:
Gỉa sử C là tổng của đa thức B với đa thức 2x4 - 3x2y + y4 + 6xz-z2 (C là đa thức bất kì không chưa biến x)
Ta có:
Thử đáp án A:
- 2x4 + 3x2y + y2 - 6xz + 5y4 + 3z2 = - 2x4 + 3x2y - y4 - 6xz + z2 + C
⇒ C = ( - 2x4 + 3x2y + y2 - 6xz + 5y4 + 3z2) - ( - 2x4 + 3x2y - y4 - 6xz + z2)
⇒ C = y2 + 6y4 + 2z2
Do C là đa thức không chưa biến x, đáp án A thỏa mãn yêu cầu bài toán
Đáp án cần chọn là: A
Câu 18: Tính giá trị của đa thức C = xy + x2y2 + x3y3 + ... + x100y100 tại x = -1; y = -1
A. C = 10
B. C = 99
C. C = 100
D. C = 101
Lời giải:
Thay x = -1; y = -1 vào biểu thức C ta có:
Đáp án cần chọn là: C
Câu 19: Tính giá trị của đa thức C = xy + x2y2 + x3y3 + ... + x100 y100 tại x = -1; y = 1
A. C = -100
B. C = 100
C. C = 0
D. C = 50
Lời giải:
Thay x = -1; y = 1 vào đa thức C ta được:
C = (-1).1 + (-1)2.12 + (-1)3.13 + ... + (-1)100.1100
C = (-1) + 1 + (-1) + 1 + ... + (-1) + 1
C = 0
Đáp án cần chọn là: C
Câu 20: Cho a, b, c là những hằng số và A + B + C = 2020. Tính giá trị của đa thức P = ax4y4 + bx3y+cxy tại x = -1; y = -1
A. P = 4040
B. P = 2020
C. P = 2002
D. P = 2018
Lời giải:
Thay x = -1; y = -1 vào biểu thức P ta được:
P = a.(-1)4.(-1)4 + b.(-1)3.(-1) + c.(-1).(-1) = A + B + C = 2020
Vậy P = 2020
Đáp án cần chọn là: B
Câu 21: Cho a, b, c là những hằng số và a + 2b + 3c = 2200. Tính giá trị của đa thức P = ax2y2 - 2bx3y4 + 3cx2y tại x = -1; y = 1
A. P = 4400
B. P = 2200
C. P = 2020
D. P = -2200
Lời giải:
Thay x = -1; y = 1 vào biểu thức P ta có:
P = a.(-1)2.12 - 2b.(-1)3.14 + 3c.(-1)2.1 = a + 2b + 3c = 2200
Đáp án cần chọn là: B
Câu 22: Tìm giá trị của đa thức N = x3 + x2y - 2x2 - xy - y2 + 3y + x-1 biết x + y - 2=0
A. N = -1
B. N = 0
C. N = 2
D. N = 1
Lời giải:
Ta có:
Vậy N = 1
Đáp án cần chọn là: D
Câu 23: Tìm giá trị của đa thức M = x3 - 2x2 - xy2 + 2xy + 2y + 2x-5 biết x + y = 2
A. M = 1
B. M = 9
C. M = 0
D. M = -1
Lời giải:
Đáp án cần chọn là: D
Câu 24: Cho M = x-(y - z)-2x + y + z-(2-x-y) và N = x-[x-(y - 2z - 2z]. Tính M-N
A. -2z + 2
B. -2x -2y -2
C. 2z - 2
D. -2x + 2y - 2
Lời giải:
Đáp án cần chọn là: C
Câu 25: Nếu 3(4x + 5y) = P thì 12(12x + 15y) bằng:
A. 12P
B. 36P
C. 4P
D. 20P
Lời giải:
Ta có:
12(12x + 15y) = 12(3.4x + 3.5y) = 12.3(4x + 5y) = 12P
Đáp án cần chọn là: A
Câu 26: Cho P = xyz + x2y2 z2 + x3y3 z3 + .... + x2020y2020z2020. Tính P biết x = y = 1; z = -1
A. P = -2020
B. P = 0
C. P = 2020
D. P = 1010
Lời giải:
Thay x = y = 1; z = -1 vào biểu thức P ta có:
P = 1.1.(-1) + 12.12.(-1)2 + 13.13.(-1)3 + .... + 12020.12020.(-1)2020
= (-1) + 1 + (-1) + 1 + ... + (-1) + 1=0
Đáp án cần chọn là: B