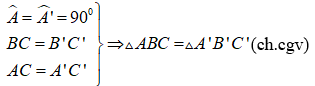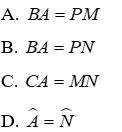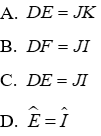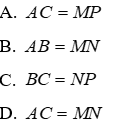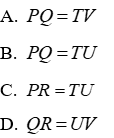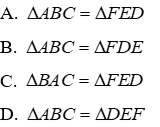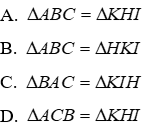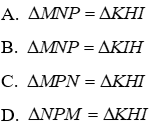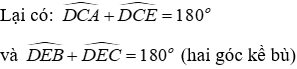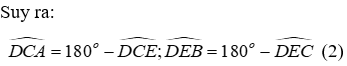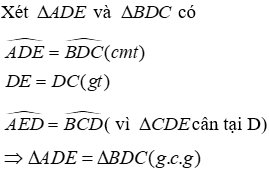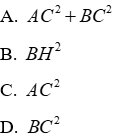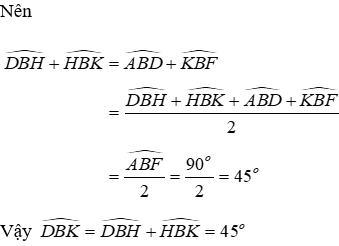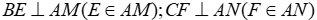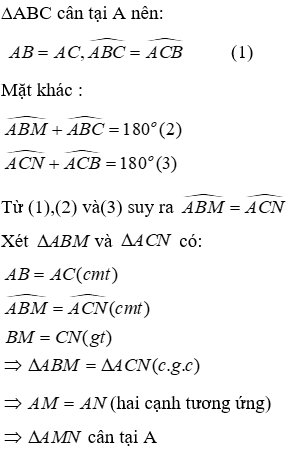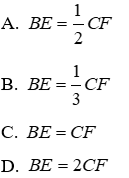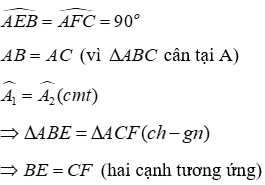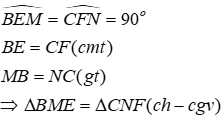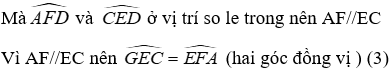Toán học 7 Bài 34: Các trường hợp bằng nhau của tam giác vuông
Lý thuyết tổng hợp Toán học lớp 7 Bài 34: Các trường hợp bằng nhau của tam giác vuông, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 34: Các trường hợp bằng nhau của tam giác vuông
A. Lý thuyết
1. Các trường hợp bằng nhau đã biết của tam giác vuông
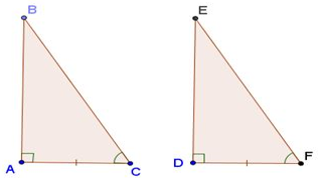
• Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau (cạnh – góc – cạnh).
• Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
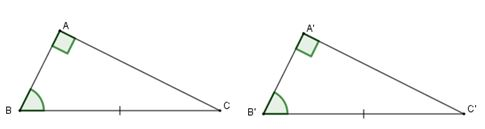
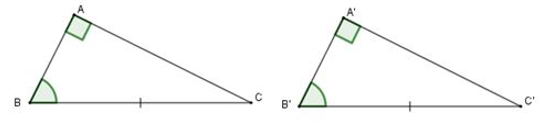
• Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đó bằng nhau.
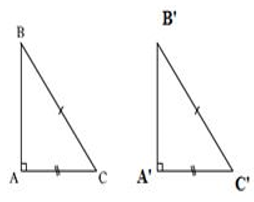
2. Trường hợp bằng nhau về cạnh huyền, cạnh góc vuông
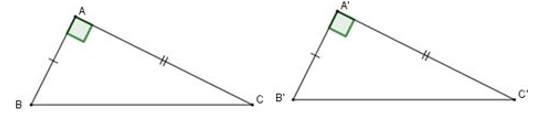
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
3. Bài tập vận dụng
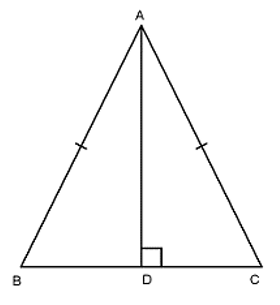
Bài 1: Cho tam giác ABC cân tại A, kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A?
Hướng dẫn giải:
Xét hai tam giác vuông ADB và ADC đều vuông tại D có
AD chung
AB = AC (tam giác ABC cân tại A)
Nên ΔADB = ΔADC (cạnh huyền – cạnh góc vuông)
Suy ra ∠BAD = ∠CAD (góc tương ứng bằng nhau)
Mà tia AD nằm giữa tia AB và AC
Vậy AD là tia phân giác của góc BAC.
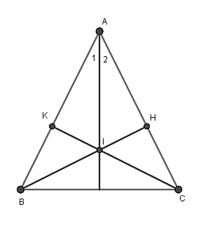
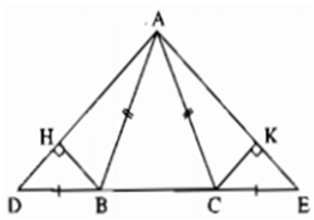
Bài 2: Cho tam giác ABC cân tại A, kẻ BH ⊥ AC, CK ⊥ AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.
Hướng dẫn giải:
Xét hai tam giác AHB vuông tại H và AKC vuông tại K có:
AB = AC (tam giác ABC cân tại A)
chung
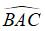
Nên ΔAHB = ΔAKC (cạnh huyền – góc nhọn)
Suy ra AH = AK (cạnh tương ứng)
Xét tam giác AHI vuông tại H và AKI vuông tại K ta có:
AI là cạnh chung
AH = AK
Nên ΔAHI = ΔAKI (cạnh huyền - cạnh góc vuông)
⇒ ∠A1 = ∠A2 (góc tương ứng bằng nhau)
Do đó AI là tia phân giác góc A
B. Bài Tập
Câu 1: Cho tam giác ABC và tam giác NPM có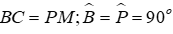 
. Cần thêm một điều kiện gì để tam giác ABC và tam giác NPM bằng nhau theo trường hợp cạnh huyền - góc vuông?
Lời giải:
Ta có tam giác ABC và tam giác NPM có 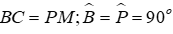mà BC; PM là hai cạnh góc vuông của hai tam giác ABC và tam giác NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là CA = MN
Đáp án cần chọn là: C
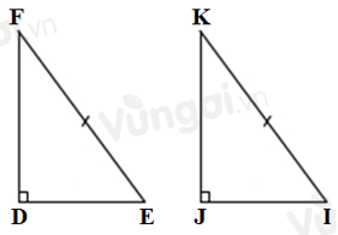
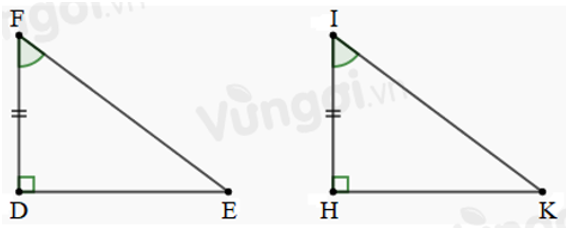
Câu 2: Cho tam giác DEF và tam giác JIK có: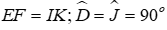 
. Cần thêm một điều kiện gì để ΔDEF = ΔJIK theo trường hợp cạnh huyền - góc vuông?
Lời giải:
Ta có: tam giác DEF và tam giác JIK có: 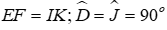mà EF; IK là hai cạnh huyền của hai tam giác DEF và JIK nên để ΔDEF = ΔJIK theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh góc vuông bằng nhau là DE = JI hoặc DF = JK
Đáp án cần chọn là: C
Câu 3: Cho tam giác ABC và tam giác MNP có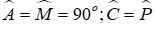 
. Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề?
Lời giải:
Ta có: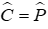 
mà góc C và góc P là hai góc nhọn kề của hai tam giác ABC và MNP
Do đó: để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn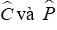 
của hao tam giác này bằng nhau, tức là bổ sung thêm điều kiện AC = MP
Đáp án cần chọn là: A
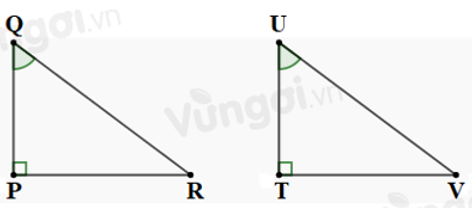
Câu 4: Cho tam giác PQR và tam giác TUV có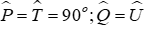 
. Cần thêm một điều kiện gì để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề:
Lời giải:
Ta có: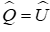 
mà góc Q và góc U là hai góc nhọn kề của hai tam giác PQR và tam giác TUV
Do đó: để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn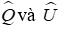 
của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện PQ = TU
Đáp án cần chọn là: B
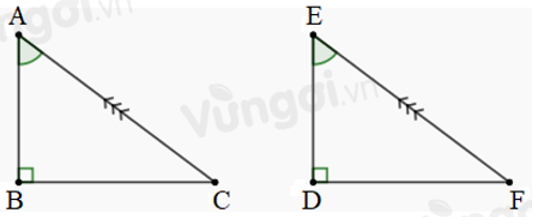
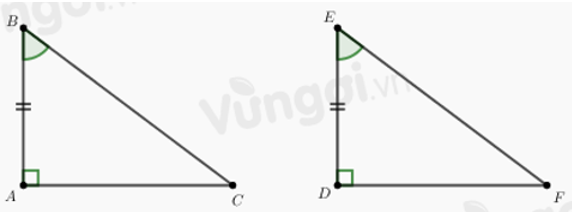
Câu 5: Cho tam giác ABC và tam giác DEF có: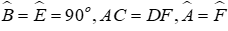 
. Phát biểu nào trong các phát biểu sai đây là đúng
Lời giải:
Xét tam giác ABC và tam giác FED có:
Đáp án cần chọn là: A
Câu 6: Cho tam giác ABC và tam giác DEF có: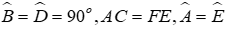 
.
Tính độ dài AB biết DE = 5cm
A. 4 cm
B. 3 cm
C. 5 cm
D. 6 cm
Lời giải:
Xét tam giác ABC và EDF có:
Đáp án cần chọn là: C
Câu 7: Cho tam giác ABC và KHI có: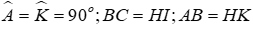 
. Phát biểu nào trong các phát biểu sau là đúng:
Lời giải:
Xét tam giác ABC và tam giác KHI có:
Đáp án cần chọn là: A
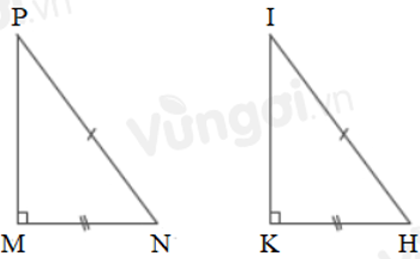
Câu 8: Cho tam giác MNP và KHI có: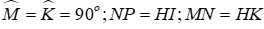 
. Chọn khẳng định đúng.
Lời giải:
Xét tam giác MNP và KHI có:
Đáp án cần chọn là: A
Câu 9: Cho tam giác ABC và tam giác DEF có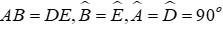 
. Biết AC = 9cm. Độ dài DF là:
A. 10 cm
B. 5 cm
C. 9 cm
D. 7 cm
Lời giải:
Đáp án cần chọn là: C
Câu 10: Cho tam giác ABC và tam giác DEF có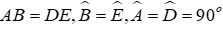 
. Biết AB = 9cm, AB = 12cm. Độ dài EF là:
A. 12 cm
B. 9 cm
C. 15 cm
D. 13 cm
Lời giải:
Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
⇒ ∆ABC = DEF (cạnh góc vuông - góc nhọn kề)
⇒ BC = EF = 15cm (hai cạnh tương ứng)
Đáp án cần chọn là: C
Câu 11: Cho tam giác DEF và tam giác HKI có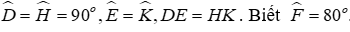 
. Số đo góc I là:
Lời giải:
Đáp án cần chọn là: C
Câu 12: Cho tam giác DEF và tam giác HKI có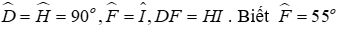 
. Số đo góc K là:
Lời giải:
Áp dụng định lí tổng ba góc của một tam giác vào ∆DEF, ta có:
Đáp án cần chọn là: B
Câu 13: Cho hình vẽ. Chọn câu đúng
Lời giải:
Vì tam giác ABC cân tại A (do AB = AC) nên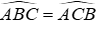 
(tính chất)(1)
Lại có: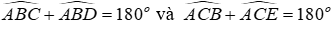 
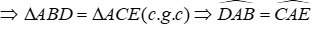
(hai góc kề bù)
(hai góc tương ứng)
Đáp án cần chọn là: D
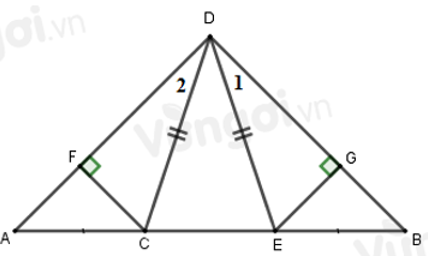
Câu 14: Cho hình vẽ sau với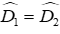 
. Chọn câu sai
Lời giải:
Vì tam giác CDE cân tại D (do DC = DE) nên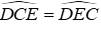 
(tính chất tam giác cân) (1)
Do đó đáp án D sai
Đáp án cần chọn là: D
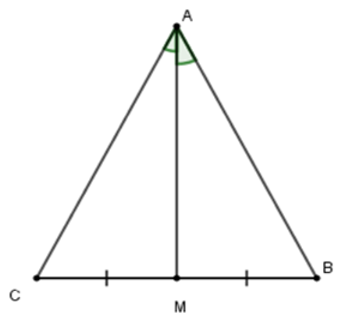
Câu 15: Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Khi đó, tam giác ABC là tam giác gì?
Lời giải:
Tam giác ABC có AM vừa là đường trung tuyến vừa là đường phân giác nên ∆BAC cân tại A
Đáp án cần chọn là: D
Câu 16: Cho tam giác ABC cân tại A có: AH ⊥ BC tại H. Tính số đo góc BAH biết 
Lời giải:
Đáp án cần chọn là: B
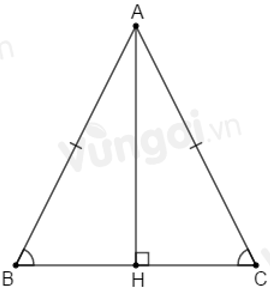
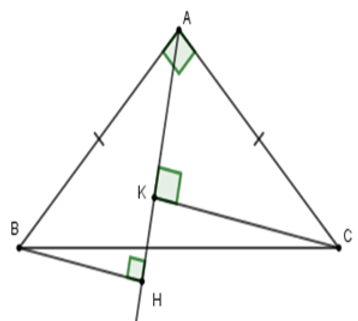
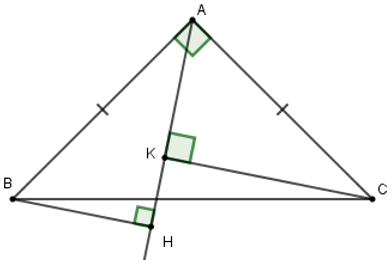
Câu 17: Cho tam giác ABC vuông cân tại A. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông goc với đường thẳng d. Khi đó BH2 + CK2 bằng:
Lời giải:
Vì ∆ABC vuông cân tại A nên AB = AC (tính chất)
Đáp án cần chọn là: C
Câu 18: Cho tam giác ABC vuông cân tại A, có AC = 8cm. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông góc với đường thẳng d. Khi đó BH2 + CK2 bằng:
A. 46
B. 16
C. 64
D. 48
Lời giải:
Vì ∆ABC vuông cân tại A nên AB = AC (tính chất)
Đáp án cần chọn là: C
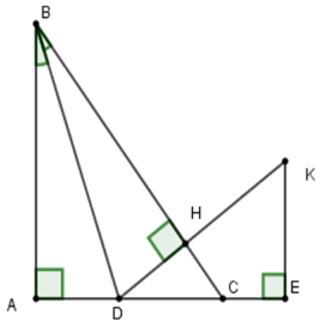
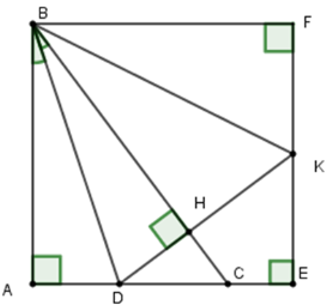
Câu 19: Cho tam giác ABC vuông tại A (AB > AC). Tia phân giác của góc B cắt AC ở D. Kẻ DH vuông góc với BC. Trên tia AC lấy E sao cho AE = AB. Đường thẳng vuông góc AE tại E cắt tia BH tại K
19.1: Chọn câu đúng
Lời giải:
(hai cạnh tương ứng)
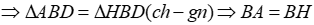
Đáp án cần chọn là: D
19.2: Tính số đo góc DBK
Lời giải:
+ Qua B kẻ đường thẳng vuông góc với EK cắt EK tại F
Xét hai tam giác vuông BHK và BFK có:
Đáp án cần chọn là: A
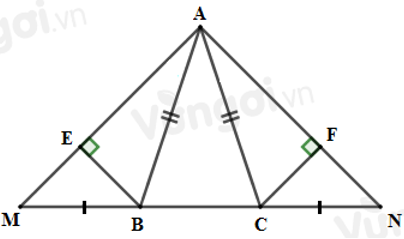
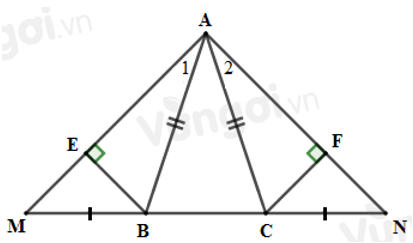
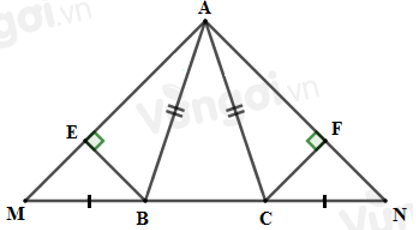
Câu 20: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho MN = BC. Kẻ 
20.1: Tam giác AMN là tam giác gì?
A. Vuông cân
B. Cân
C. Đều
D. Vuông
Lời giải:
Đáp án cần chọn là: B
20.2: So sánh BE và CF
Lời giải:
Sử dụng kết quả câu trước ta có: ∆ABM = ∆ACN suy ra Â1 = Â2 (hai góc tương ứng)
Xét hai tam giác vuông ABE và ACF có:
Đáp án cần chọn là: C
20.3: Chọn câu đúng
Lời giải:
Sử dụng kết quả câu trước ∆ABE = ∆ACF nên BE = CF (hai cạnh tương ứng)
Xét hai tam giác vuông BME và CNF có:
Đáp án cần chọn là: A
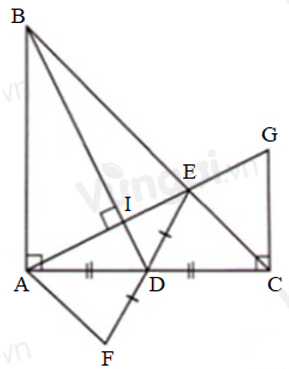
Câu 21: Cho tam giác ABC vuông cân tại A và D là trung điểm AC. Từ A kẻ đường vuông góc với BD, cắt BC tại E. Chọn đáp án đúng
Lời giải:
Từ C dựng đường thẳng vuông góc với AC cắt AE tại G. Trên tia đối của tia DE lấy điểm F sao cho DE = DF. Gọi I à giao điểm của AE và BD
Mà AD = CD (vì D là trung điểm của AC) nên CD = CG
∆ABC vuông cân tại A nên
Đáp án cần chọn là: C
