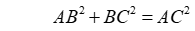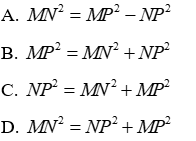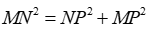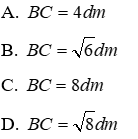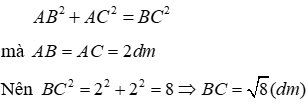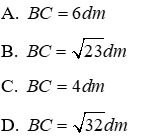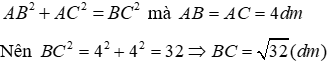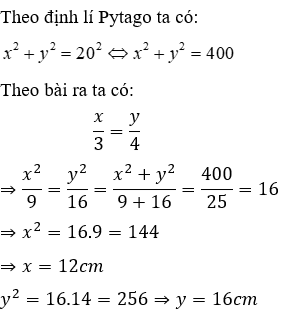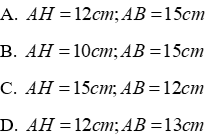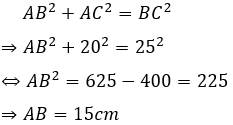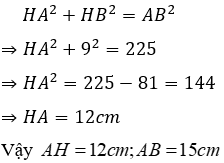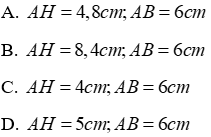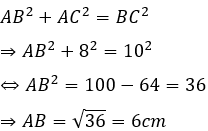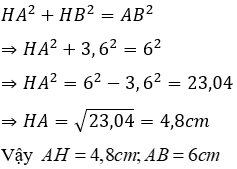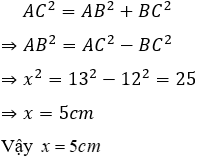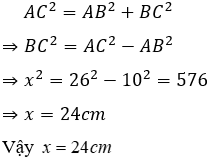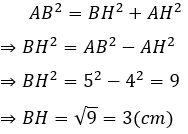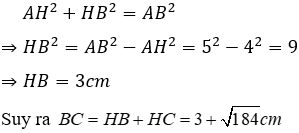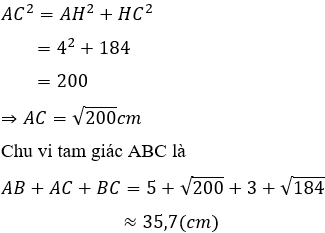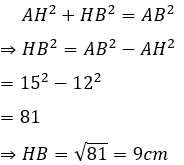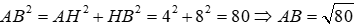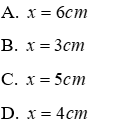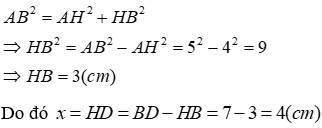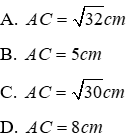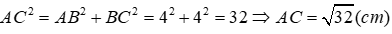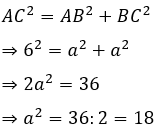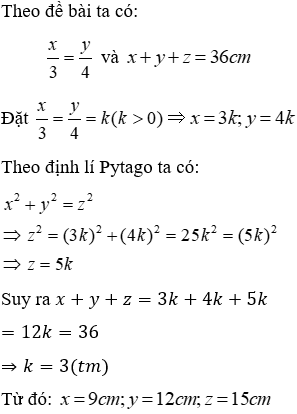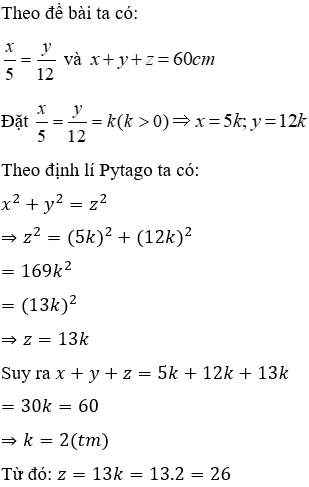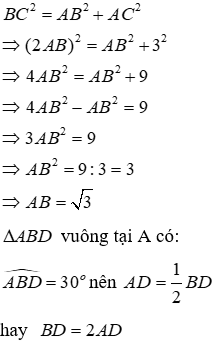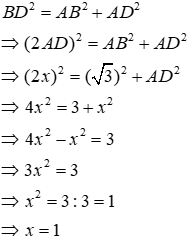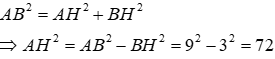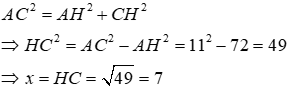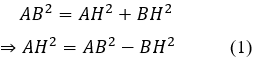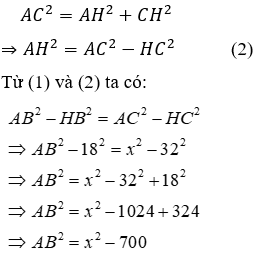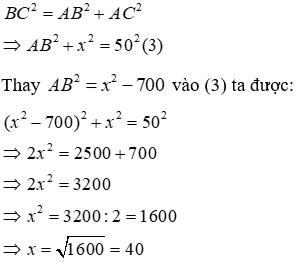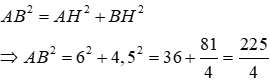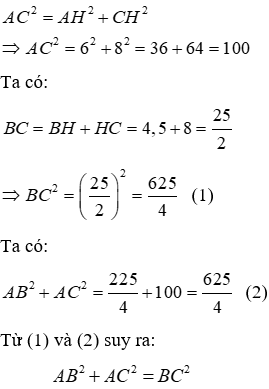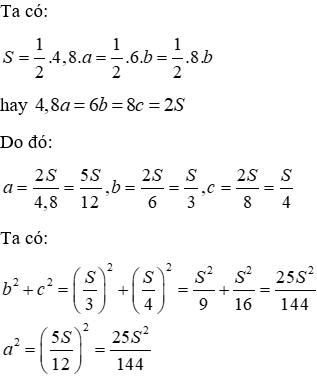Toán học 7 Bài 33: Định lí Pi-ta-go

Lý thuyết tổng hợp Toán học lớp 7 Bài 33: Định lí Pi-ta-go, chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.

483

Tải tài liệu

« Trang trước

Trang sau »

Bài 33: Định lí Pi-ta-go

A. Lý thuyết

1. Định lý Pytago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

ΔABC vuông tại A ⇒ BC² = AB² + AC²

2. Định lý Pytago đảo

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

ΔABC có BC² = AB² + AC² ∠BAC = 90^o

3. Ví dụ

Ví dụ: Nếu độ dài của hai cạnh góc vuông của tam giác vuông tăng lên 2 lần, 3 lần thì độ dài cạnh huyền thay đổi như thế nào?

Hướng dẫn giải:

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Tương tự, khi độ dài cạnh góc vuông tăng lên 3 lần thì độ dài cạnh huyền cũng tăng lên 3 lần.

3. Bài tập vận dụng

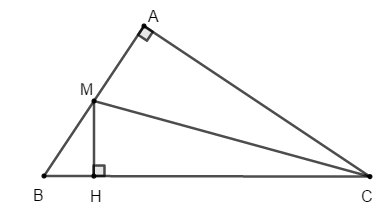
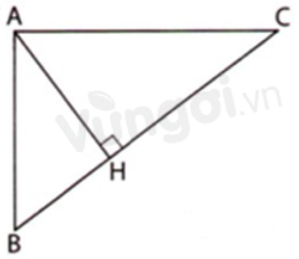
Bài 1: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, kẻ MH vuông góc với BC tại H. Chứng minh rằng CH² - BH² = AC²

Hướng dẫn giải:

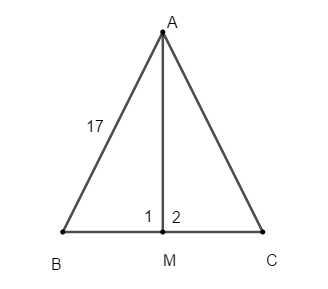
Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

Bài 2: Cho tam giác ABC cân tại A có M là trung điểm của BC. Biết AB = 17 cm, BC = 16 cm. Tính AM.

Hướng dẫn giải:

Toán lớp 7 | Lý thuyết - Bài tập Toán 7 có đáp án

B. Bài Tập

Câu 1: Cho tam giác ABC vuông tại B khi đó x = 1

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Vì tam giác ABC vuông tại B nên theo định lí Pytago có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: A

Câu 2: Cho tam giác MNP vuông tại P khi đó:

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Vì Cho tam giác MNP vuông tại P nên theo định lí Pytago có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

Câu 3: Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2dm

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

Câu 4: Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 4dm

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

Câu 5: Một tam giác có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông

A. 12 cm; 24 cm

B. 10 cm; 22 cm

C. 10 cm; 24 cm

D. 15 cm; 24 cm

Lời giải:

Gọi độ dài hai cạnh góc vuông là x; y (x; y > 0)

Trắc nghiệm Định lí Pi-ta-go

Vậy các cạnh góc vuông có độ dài 10 cm; 24 cm

Đáp án cần chọn là: C

Câu 6: Một tam giác có cạnh huyền bằng 20cm độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Tính độ dài các cạnh góc vuông

A. 9 cm; 12 cm

B. 10 cm; 16 cm

C. 12 cm; 16 cm

D. 12 cm; 14 cm

Lời giải:

Gọi độ dài hai cạnh góc vuông là x; y (x; y > 0)

Trắc nghiệm Định lí Pi-ta-go

Vậy các cạnh góc vuông có độ dài 12 cm; 16 cm

Đáp án cần chọn là: C

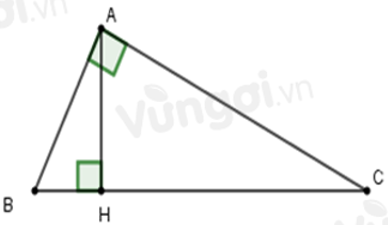
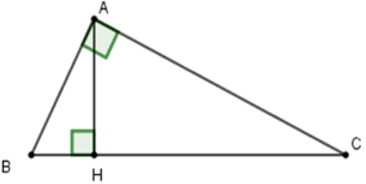
Câu 7:Cho tam giác ABC vuông ở A có AC = 20cm. Kẻ AH vuông góc BC. Biết BH = 9cm; HC = 16cm. Tính AB,AH

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Ta có: BC = BH + HC = 9 + 16 = 25cm

Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:

Trắc nghiệm Định lí Pi-ta-go

Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: A

Câu 8: Cho tam giác ABC vuông ở A có AC = 8cm. Kẻ AH vuông góc BC. Biết BH = 3,6cm; HC = 6,4cm. Tính AB,AH

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Ta có: BC = BH + HC = 3,6 + 6,4 = 10cm

Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:

Trắc nghiệm Định lí Pi-ta-go

Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: A

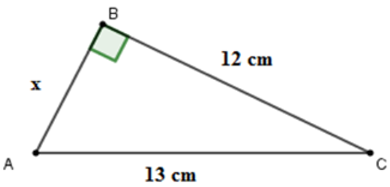
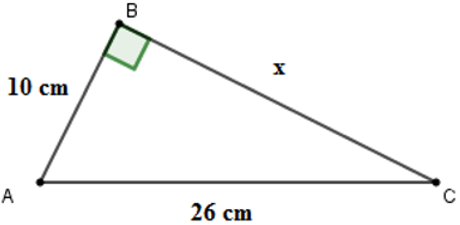
Câu 9: Cho hình vẽ . Tính x

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

Câu 10: Cho hình vẽ. Tính x

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

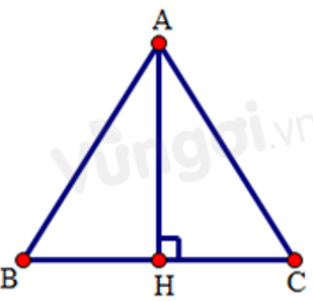
Câu 12: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH = 4cm, AB = 5cm

12.1: Tính BH

A. 2 (cm)

B. 5 (cm)

C. 3 (cm)

D. 4 (cm)

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lý Pytago vào tam giác ABH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: C

12.2: Chu vi tam giác ABC

A. 18 (cm)

B. 15(cm)

C. 16 (cm)

D. 20(cm)

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng kết quả câu trước có BH = 3cm

ΔABC cân tại A nên AB = AC = 5cm

Áp dụng định lí Pytago vào tam giác ACH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: C

Câu 13: Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi ΔABC biết AB = 5cm, AH = 4cm, HC = √184 cm (làm tròn đến chữ số thập phân thứ nhất)

A. 30,8 cm

B. 35,7 cm

C. 31 cm

D. 31,7 cm

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago cho tam giác vuông AHC ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: B

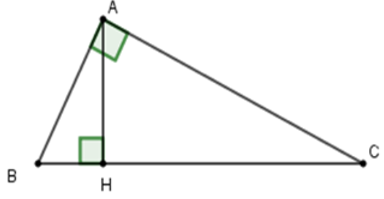
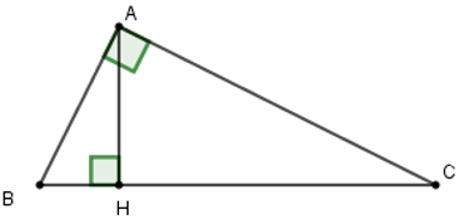
Câu 14: Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi ΔABC biết AB = 15cm, AH = 12cm, HC = 16cm

A. 62 cm

B. 60 cm

C. 64 cm

D. 58 cm

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:

Trắc nghiệm Định lí Pi-ta-go

Suy ra BC = HB + HC = 9 + 16 = 25cm

Áp dụng định lí Pytago cho tam giác vuông AHC ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: B

Câu 15:Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau

A. 15cm; 8cm; 18cm

B. 21dm; 20dm; 29dm

C. 5m; 6m; 8m

D. 2m; 3m; 4m

Lời giải:

+ Với bộ số 15cm; 8cm; 18cm ta thấy 18² = 324,15² + 8² = 289

Nên 289 < 324 hay 15² + 8² < 18²

Nên loại A

+ Với bộ số 21dm; 20dm; 29dm ta thấy 29² = 841; 21² + 20² = 841

Nên 21² + 20² = 29² hay tam giác với độ dài 21dm; 20dm; 29dm thì tam giác đó là tam giác vuông (theo định lí Pytago đảo)

+Với bộ số 5m; 6m; 8m ta thấy 8² = 64; 5² + 6² = 41 ⇒ 8² > 5² + 6²

Nên loại C

+ Với bộ số 2m; 3m; 4m ta thấy 4² = 16; 2² + 3² = 13 ⇒ 4² > 2² + 3²

Nên loại D

Đáp án cần chọn là: B

Câu 16: Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau

A. 11cm; 7cm; 8cm

B. 12dm; 15dm; 18dm

C. 9m; 12m; 15m

D. 6m; 7m; 9m

Lời giải:

+ Với bộ số 11cm; 7cm; 8cm ta thấy 11² = 121; 7² + 8² = 113 ⇒ 11² > 7² + 8²

Nên loại A

+ Với bộ số 12dm; 15dm; 18dm ta thấy 18² = 324; 12² + 15² = 369 ⇒ 12² + 15² > 18²

Nên loại B

+ Với bộ số 9m; 12m; 15m ta thấy 15² = 225; 9² + 12² = 225 ⇒ 9² + 12² = 15²

Theo định lí Pytago đảo, tam giác với ba cạnh có độ dài 9m;12m;15m là tam giác vuông

+ Với bộ số 6m; 7m; 9m ta thấy 9² = 81; 6² + 7² = 85 ⇒ 6² + 7² > 9²

Nên loại D

Đáp án cần chọn là: C

Câu 17:Cho hình vẽ. Tính x

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago cho tam giác vuông AHB ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

Câu 18: Cho hình vẽ. Tính x

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago cho tam giác vuông AHB ta được:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: D

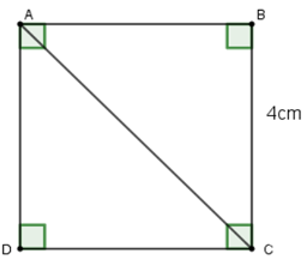
Câu 19: Cho ABCD là hình vuông cạnh 4 cm(hình vẽ). Khi đó, độ dài đường chéo AC là

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Vì ABCD là hình vuông nên AB = BC = 4cm

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: A

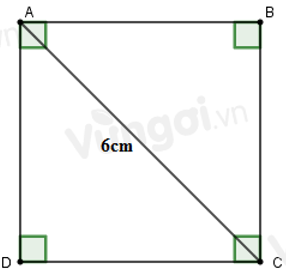
Câu 20: Cho ABCD là hình vuông cạnh x cm(hình vẽ). Biết độ dài đường chéo AC là 6 cm. Bình phương độ dài cạnh của hình vuông là

Trắc nghiệm Định lí Pi-ta-go

A. 20

B. 18

C. 6

D. 16

Lời giải:

Vì ABCD là hình vuông nên AB = BC = a(cm)

Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:

Trắc nghiệm Định lí Pi-ta-go

Vậy bình phương độ dài cạnh của hình vuông là 18

Đáp án cần chọn là: B

Câu 21:Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 3:4 và chu vi tam giác bằng 36 cm

A. 9 cm

B. 12 cm

C. 15 cm

D. 16 cm

Lời giải:

Gọi độ dài hai cạnh góc vuông là x; y (y > x > 0) (cm) và độ dài cạnh huyền là z (z > y) (cm)

Trắc nghiệm Định lí Pi-ta-go

Vậy cạnh huyền dài 15cm

Đáp án cần chọn là: C

Câu 22: Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 5:12 và chu vi tam giác bằng 60 cm

A. 20 cm

B. 24 cm

C. 26 cm

D. 10 cm

Lời giải:

Gọi độ dài hai cạnh góc vuông là x; y (y > x > 0) (cm) và độ dài cạnh huyền là z (z > y) (cm)

Trắc nghiệm Định lí Pi-ta-go

Vậy cạnh huyền dài 26cm

Đáp án cần chọn là: C

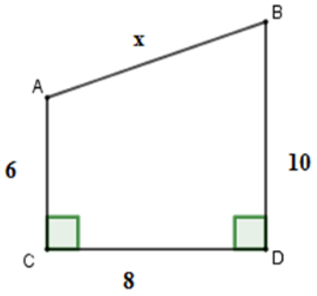
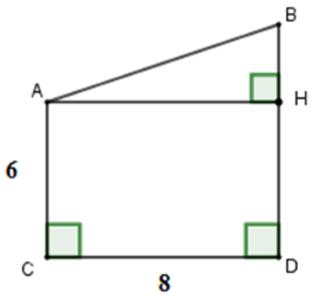
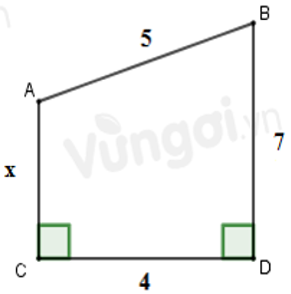
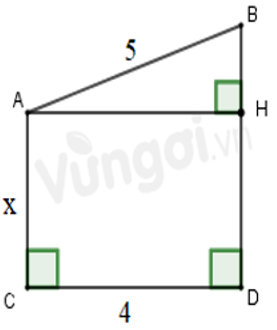
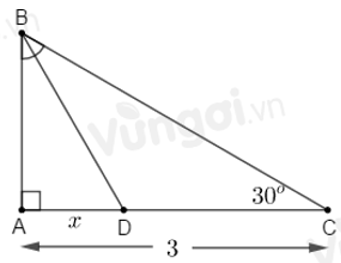
Câu 23: Tính x trong hình vẽ sau:

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago vào ΔABC vuông tại A ta có:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago vào ΔABD vuông tại A ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: C

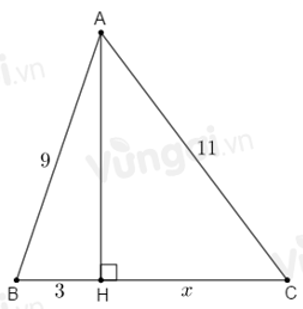
Câu 24: Tính x trong hình vẽ sau:

Trắc nghiệm Định lí Pi-ta-go

Lời giải:

Áp dụng định lí Pytago vào ΔABH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago vào ΔACH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: B

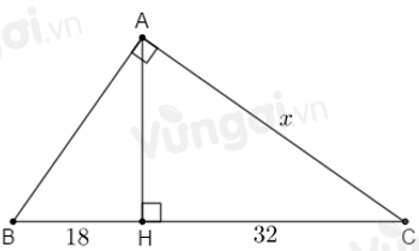
Câu 25: Tính x trong hình vẽ sau:

Trắc nghiệm Định lí Pi-ta-go

A. 36

B. 40

C. 42

D. 30

Lời giải:

Áp dụng định lí Pytago vào ΔABH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Áp dụng định lí Pytago vào ΔACH vuông tại H ta có:

Trắc nghiệm Định lí Pi-ta-go

Ta có: BC = BH + CH = 18 + 32 = 50

Áp dụng định lí Pytago vào tam giác ABC vuông tại A ta có:

Trắc nghiệm Định lí Pi-ta-go

Đáp án cần chọn là: B

Câu 26: Cho tam giác ABC có 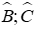Trắc nghiệm Định lí Pi-ta-go là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm; BH = 4,5cm; HC = 8cm. Khi đó ΔABC là tam giác gì?