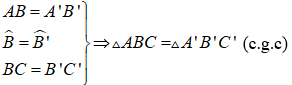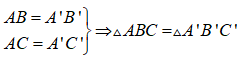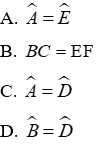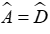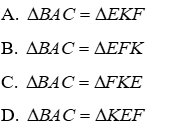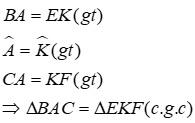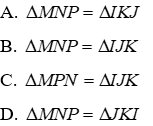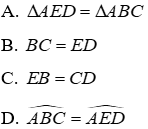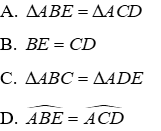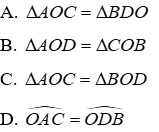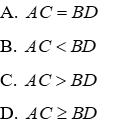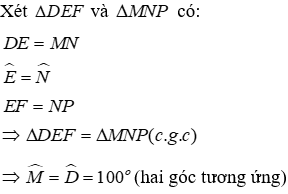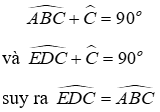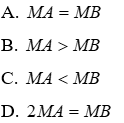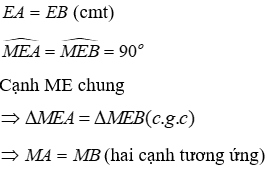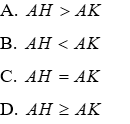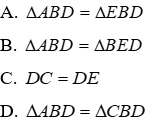Toán học 7 Bài 32: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
Lý thuyết tổng hợp Toán học lớp 7 Bài 32: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c), chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 7. Hy vọng bộ tổng hợp lý thuyết Toán học lớp 7 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 7.
Bài 32: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c)
A. Lý thuyết
1. Vẽ tam giác biết hai cạnh và góc xen giữa
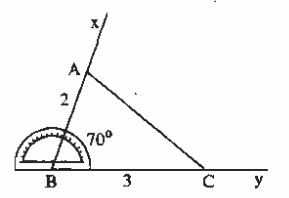
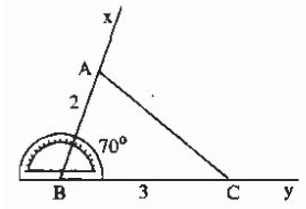
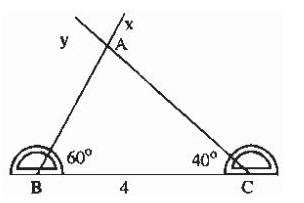
Bài toán: Vẽ tam giác ABC biết AB = 2cm, BC = 3cm, ∠B = 70o
• Vẽ góc ∠xBy = 70o.
• Trên tia By lấy điểm A sao cho BA = 2cm.
• Trên tia By lấy điểm C sao cho BC = 3cm.
• Vẽ đoạn thẳng AC ta được tam giác ABC.
Lưu ý: Ta gọi góc B là góc xen giữa hai cạnh AB và BC. Khi nói hai cạnh và góc xen giữa, ta hiểu góc này là góc ở vị trí xen giữa hai cạnh đó.
2. Trường hợp bằng nhau cạnh – góc – cạnh
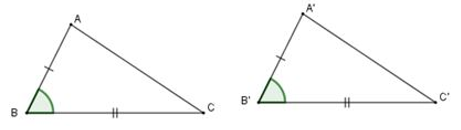
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
ΔABC và ΔA'B'C' có:
3. Hệ quả
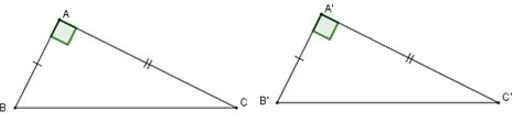
Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Cho tam giác ABC vuông tại A, tam giác A’B’C’ vuông tại A’, khi đó:
4. Ví dụ
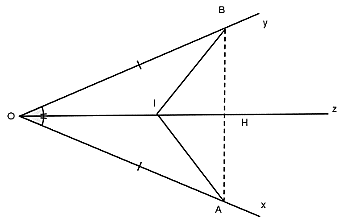
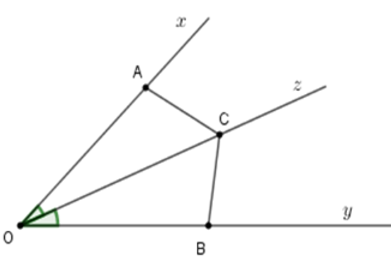
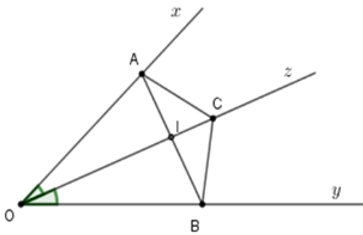
Ví dụ:Cho góc xOy với điểm I nằm trên tia phân giác Oz, lấy điểm A trên Ox, B trên Oy sao cho OA = OB
a) Chứng minh ΔAOI = Δ BOI
b) Đoạn thẳng AB cắt Oz tại H, chứng minh rằng ΔAIH = ΔBIH
c) Chứng minh rằng tam giác AIH và BIH đều là tam giác vuông
Hướng dẫn giải:
4. Bài tập vận dụng
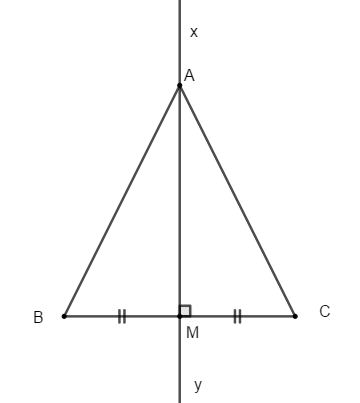
Bài 1: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC
Hướng dẫn giải:
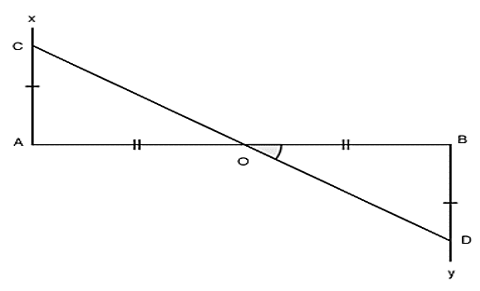
Bài 2: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.
a) Chứng minh rằng: ΔAOC = ΔBOD
b) Chứng minh O là trung điểm của CD
Hướng dẫn giải:
B. Bài Tập
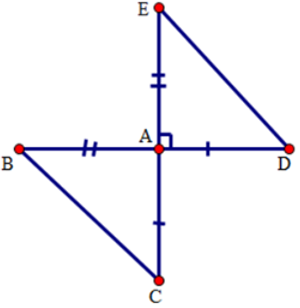
Câu 1: Cho tam giác ABC và tam giác MHK có: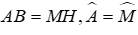 
. Cần thêm một điều kiện gì để tam giác ABC và tam giác MHK bằng nhau theo trường hợp cạnh-góc-cạnh
Lời giải:
Để tam giác ABC và tam giác MHK bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là: AC = MK
Đáp án cần chọn là: C
Câu 2: Cho tam giác ABC và tam giác DEF có: AB = DE, AC = DF. Cần thêm một điều kiện gì để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh-góc-cạnh
Lời giải:
Để tam giác ABC và tam giác DEF bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về cạnh kề đó là: 
Đáp án cần chọn là: C
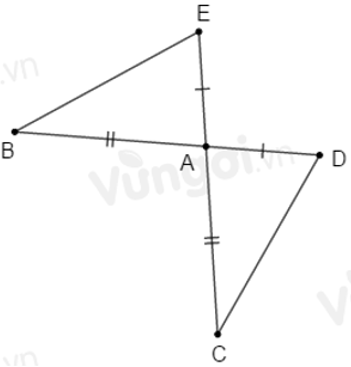
Câu 3: Cho tam giác BAC và tam giác KEF có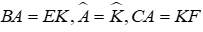 
. Phát biểu nào trong các phát biểu sau đây đúng
Lời giải:
Xét tam giác BAC và tam giác KEF có:
Đáp án cần chọn là: A
Câu 4: Cho tam giác MNP và tam giác IJK có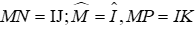 
. Phát biểu nào trong các phát biểu sau đây đúng
Lời giải:
Đáp án cần chọn là: B
Câu 5: Cho đoạn thẳng BD và EC vuông góc với nhau tại A sao cho AB = AE, AD = AC, AB < AC.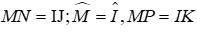 
. Phát biểu nào trong các phát biểu sau đây sai.
Lời giải:
Đáp án cần chọn là: C
Câu 6: Cho đoạn thẳng BD và EC cắt nhau tại A sao cho AB = AC, AD = AE, AB > AD. Phát biểu nào trong các phát biểu sau đây sai.
Lời giải:
Đáp án cần chọn là: C
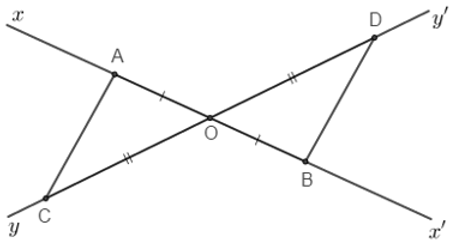
Câu 8: Cho hai đường thẳng xx' ,yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C,D sao cho O là trung điểm CD (A ∈ Ox; C ∈ Oy)
8.1: Chọn câu đúng
Lời giải:
Đáp án cần chọn là: D
8.2: So sánh AC và BD
Lời giải:
Đáp án cần chọn là: A
Câu 9: Cho tam goác DEF và tam giác HKG có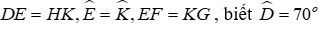 
. Số đo góc H là:
Lời giải:
Đáp án cần chọn là: A
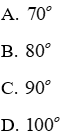
Câu 10: Cho tam goác DEF và tam giác MNP có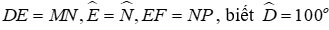 
. Số đo góc M là:
Lời giải:
Đáp án cần chọn là: D
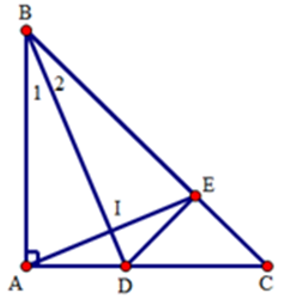
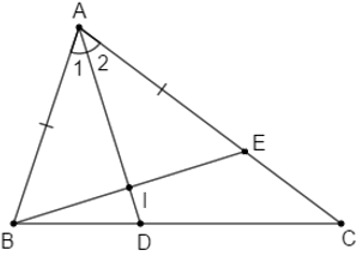
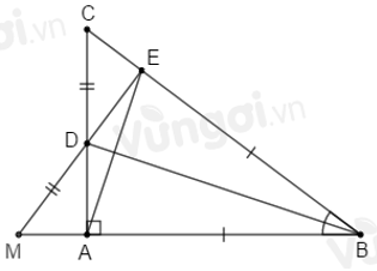
Câu 11: Cho tam giác ABC có Â = 90°, tia phân giác BD của góc B (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Hai góc nào sau đây bằng nhau
Lời giải:
Trong các tam giác ABC và EDC vuông tạo A và E, ta có:
Đáp án cần chọn là: C
Câu 12: Cho tam giác ABC có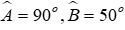 
, tia phân giác BD của góc B (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Tính số đo góc EDC
Lời giải:
Đáp án cần chọn là: C
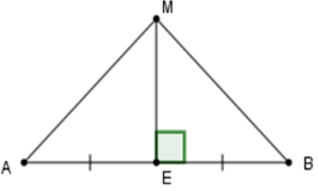
Câu 13: Cho đoạn thẳng AB, trên đường trung trực d của đoạn AB lấy điểm M. So sánh AM và BM
Lời giải:
Đường trung trực của AB vuông góc với AB tại trung điểm E. Do đó ME ⊥ AB, EA = EB
Xét tam giác MEA và tam giác MEB có:
Đáp án cần chọn là: A
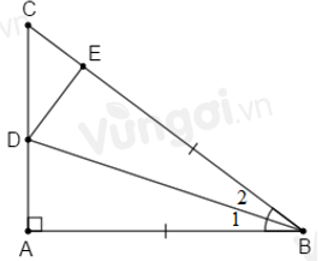
Câu 14: Cho tam giác ABC có AC > AB, tia phân giác của góc A cắt BC ở D. Trêm cạnh AC lấy E sao cho AE = AB. Chọn câu đúng
Lời giải:
Từ (1) và (2) suy ra AD là đường trung tuyến của BE
Đáp án cần chọn là: C
Câu 15: Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O
15.1: Chọn câu đúng
Lời giải:
Vì BD và CE là tia phân giác của góc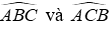 
nên
Đáp án cần chọn là: D
Lời giải:
Mà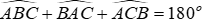 
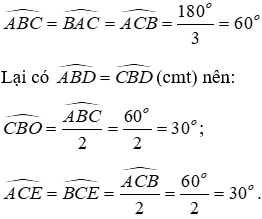
(định lý tổng ba góc trong tam giác) nên
Xét tam giác BOC có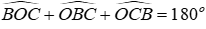 
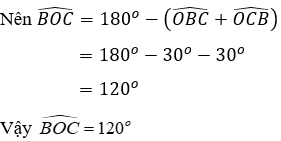
(định lý tổng ba góc trong tam giác)
Đáp án cần chọn là: C
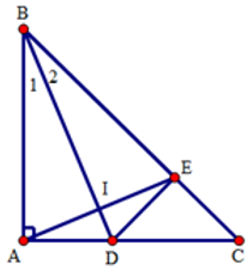
Câu 16: Cho góc nhọn xOy và Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A và trên tia Oy lấy điểm B sao cho OA = OB. Gọi C là một điểm bất kì trên tia Oz
16.1: Chọn câu sai
Lời giải:
Đáp án cần chọn là: A
16.2: Gọi I là giao của AB và Oz. Tính góc AIC
Lời giải:
Đáp án cần chọn là: B
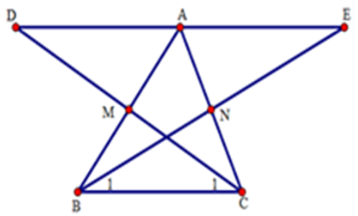
Câu 17: Cho tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Trên tia đối của tia MC lấy D sao cho MD = MC. Trên tia đối của tia NB lấy điểm E sao cho NE = NB
(I) ΔAMD = ΔBMC
(II) ΔANE = ΔCNB
(III) A, D, E thẳng hàng
(IV) A là trung điểm của đoạn thẳng DE
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 2
C. 4
D. 3
Lời giải:
Như vậy qua A có hai đường thẳng AD, AE cùng song song với BC.
Do đó D, A, E thẳng hàng (1) nên (III) đúng
(IV) Ta có: AD = BC (do ΔAMD = ΔBMC); AE = BC (do ΔANE = ΔCNB) nên AD = AE (2)
Từ (1) và (2) suy ta A là trung điểm DE
Vậy cả (I), (II), (III), (IV) đều đúng
Đáp án cần chọn là: C
Câu 18: Cho tam giác ABC, kẻ BD vuông góc với AC, kẻ CE vuông góc AB. Trên tia đối của tia BD lấy điểm H sao cho BH = AC. Trên tia đối của tia CE, lấy điểm K sao cho CK = AB. So sánh AH, AK
Lời giải:
Đáp án cần chọn là: C
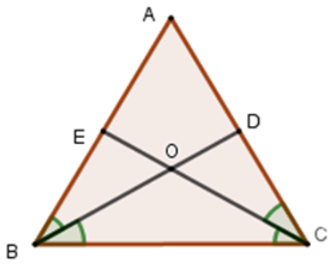
Câu 19: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E,F lần lượt là điểm thuộc đoạn AD và BC sao cho AE= BF. Cho OE = 2cm, tính EF
A. 4 cm
B. 2 cm
C. 3 cm
D. 3,5 cm
Lời giải:
⇒ ΔOBF = ΔOAE(c.g.c) nên OE = OF (hai cạnh tương ứng) và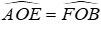 
(hai góc tương ứng)
Suy ra ba điểm F; O; E thẳng hàng và OE = OF nên O là trung điểm của EF nên EF = 2.OE = 4 cm
Đáp án cần chọn là: A
Câu 20: Cho hai đoạn thẳng AB và CD cắt nhau tại O là trung điểm của mỗi đoạn thẳng đó. Lấy E,F lần lượt là điểm thuộc đoạn AD và BC sao cho AE = BF. Cho OE = 5cm, tính EF
A. 5 cm
B. 10 cm
C. 7 cm
D. 7,5 cm
Lời giải:
Suy ra ba điểm F; O; E thẳng hàng và OE = OF nên O là trung điểm của EF nên EF = 2.OE = 2.5 = 10 cm
Đáp án cần chọn là: B
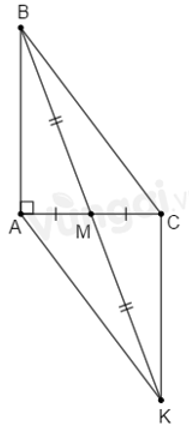
Câu 21: Cho tam giác ABC có Â = 90°, M là trung điểm của AC. Trên tia đối của tia MB lấy K sao cho MK = MB. Chọn câu đúng nhất
Lời giải:
Mà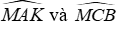 
ở vị trí so le trong nên AK//BC (B đúng)
Đáp án cần chọn là: D
Câu 22: Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho BE = AB
22.1: Chọn câu đúng
Lời giải:
Đáp án cần chọn là: A
22.2: Trên tia đối của tia DE lấy điểm M sao cho DM = DC. So sánh EC và AM
Lời giải:
Sử dụng kết quả câu trước ΔABD = ΔEBD suy ra DE = DA (hai cạnh tương ứng). Nối AM
⇒ AM = EC(hai cạnh tương ứng bằng nhau)
Đáp án cần chọn là: B
22.3: Trên tia đối của tia DE lấy điểm M sao cho DM = DC. Nôi AE, so sánh số đo 
Lời giải:
Sử dụng kết quả câu trước ΔADM = ΔEDC suy ra AD = ED; AM = EC (Các cạnh tương ứng)
Đáp án cần chọn là: C
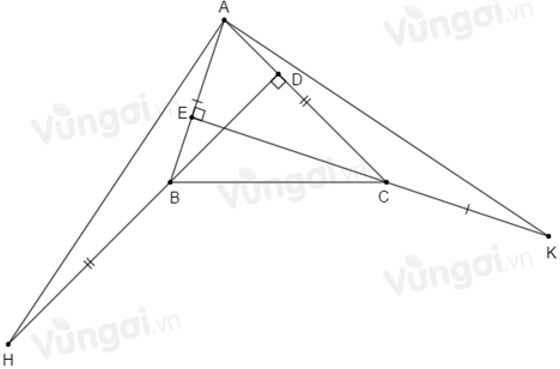
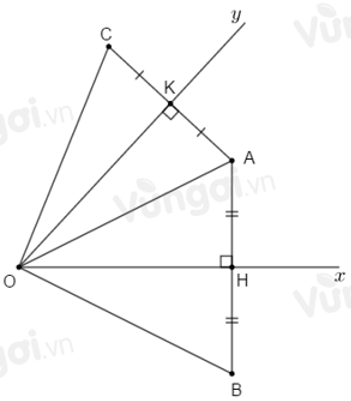
Câu 23: Cho điểm A nằm ngoài góc nhọn xOy. Vẽ AH vuông góc với Ox, trên tia đối của HA lấy điểm B sao cho HB = HA. Vẽ AK vuông góc với Oy, trên tía đối của KA lấy điểm C sao cho KC = KA.
23.1: So sánh OB; OC
Lời giải:
Đáp án cần chọn là: B
Lời giải:
Đáp án cần chọn là: C
